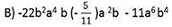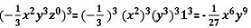Едночлен.Нормален вид на едночлен .Събиране,изваждане ,умножение и деление на едночлени .Задачи за 6 клас
1.Едночлен .Нормален вид на едночлен.Подобни едночлени .
1.1 Едночлен
Едночлен е всеки цял рационален израз ,който е произведение от числа и променливи
Примери за едночлени:
3хy; 19x2; 2xy3; −3xy2⋅(23) ⋅4x3; 5,9 xn y n (n∈N)
Едночлените могат да са само числа или само променливи
Примери: 0.12 ; 3 ; −0,5 ; x ; y ; b2 ; z n (n∈N)
Целите изрази 2a+3b; 2x−5d ; (2y+3) 2 НЕ са едночлени,защото ,те не са само произведение от числа и променливи
1.2 Нормален вид на едночлен
Да разгледаме едночлените :
- 2xy3
- −5x y2⋅(32) ⋅y3.4x3
В едночлена 2xy3 е записано едно число и всяка буква се среща само по веднъж
Всеки едночлен записан по този начин казваме,че е записан в нормален вид
Нормален (стандартен) вид има всеки едночлен записан :
- само с един числов множител ,който е пред другите множители
- произведението от еднаквите букви и променливи е записано като степен
Всеки едночлен може да се приведе в нормален вид ,като :
- намерим произведението на всички числови множители и го запишем на първо място
- като умножим всички степени с равни основи
ЧИСЛОВИЯТ МНОЖИТЕЛ на всеки едночлен записан в нормален вид наричаме КОЕФИЦИЕНТ НА ЕДНОЧЛЕНА |
Вторият едночлен −5x.y2⋅(32) .y3.4x3 не е приведен в нормален вид .
Той има коефициент −5.(32) .4=-180
КАЗВАМЕ,ЧЕ сме заменили едночлена с тъждествено равен нему едночлен |
Задача 1:Представете едночлена 0,5 х 4.z(−10 x 2z 2) в нормален вид и определете неговият коефициент .
Решение
0,5 х 4z(−10 x2z2)=−0,5.4.10xx2zz2 =−20x3z3
Коефициентът на този едночлен е −20.
Задача 2:Представете едночлена xy3z2x2z2y6 в нормален вид и определете неговият коефициент:
Решение
x y3z2x2z2y6 = xx2y3y6z2z2 = x3 .y9. z4
Коефициентът на този едночлен е 1.
Задача 3:Ако a и b са параметри ,а x и y са променливи ,намерете нормалният вид на едночлена 2х2a4xy3b1,5ay и определете неговият коефициент
Решение
2х2a4xy3b1,5ay =2.4.1,5. аabх2x y3y= 12а2bх3y4
Коефициентът на този едночлен е 12а2b
Задача 4.Намерете числената стойност на едночлена 3а3b3b2a за а= -2,b=0,5
Решение
За да работим бързо и рационално :
- намираме стандартният вид на едночлена
- заместваме в него , дадените стойности за а и b .
За а= -2,b=0,5 , числената стойност на израза е 3а3b3b2a =3а4b5=3( -2)4 2-5= 1,5
Задача 5 .Намерете числената стойност на едночлена 2х3y2х.0,20y ,ако x=2 и y=-1.
Решение
Нормалният вид на едночлена е 2х3y2х.0,20y=0,4х4y3
За х= 2,y=-1 , числената стойност на израза 0,4х4y3 =0,4 .16.(-1)=-6,4
1.3 Степен на едночлен
1
СБОРЪТ от степенните показатели на ПРОМЕНЛИВИТЕ в даден едночлен се нарича степен на едночлена |
Примери :
−x4y5 е едночлен от 9-та степен ,защото 4+5 =9 ;
−3xy5z6 е едночлен от 12 -та степен,защото 1+5+6 =12 ;
10z e едночлен от първа степен ;
0,02 е едночлен от нулева степен15bxy6 ,където b е параметър е от 7 степен ,защото 1+6=7
Примери :В дадената таблица всички букви са променливи .
Едночлен | Нормален вид | Коефициент | Степен |
6x2y(−2)3xy4 | -48x3y5 | -48 | 8 |
а2b4bcа ; | а3b5c | 1 | 9 |
-2y.(0,5y) | -y2 | -1 | 2 |
5.20 | 100 | 100 | 0 |
1
1.4 Подобни едночлени.Събиране и изваждане на подобни едночлени .
1
ЕДНОЧЛЕНИ ,които имат един и същ нормален вид,или се различават само по коефициентите си се наричат ПОДОБНИ ЕДНОЧЛЕНИ |
Подобни са едночлените :
- 12х и 15х
- 3yх3 и 15yх3
- 3xcxc и 3x 2c 2 ;
- 9 и −9;
Не са подобни едночлените : 3a2b и 12ab2
Ако два подобни едночлена имат равни коефициенти ,то те се наричат равни едночлени
Примери : 2х2 и 2хх
Ако два подобни едночлена имат противоположни коефициенти ,то те се наричат противоположни едночлени
Примери : - 2а2 и 2а2; : - 3n и 3n ;- xy и xy
Едночлен | Подобен на дадения | Противоположен на дадения | Равен на дадения |
(-1)3x |
|
|
|
а3b5c |
|
|
|
-4y.y4 |
|
|
|
(−2)3xy |
|
|
|
Подобни едночлени събираме или изваждане като :
Първо - съберем или извадим коефициентите на едночлените ;
Второ - запишем променливите без промяна
Примери :
2х+3х =(2+3)х = 5х
7х2 +0,5 х2 = (7+0,5) х2 = 7,5 х2
10х-3х =(10-3)х = 7х
23х2 -21 ,5 х2 = (23-21,5) х2 = 2,5 х2
Сборът на два противоположни едночлена е нула
Примери :
х2 - х2 = 0 ;
2y -2y =0
ВАЖНО! :Правилата за разкриване на скоби са същите ,както при действия с рационални числа
Примери :
х +(−)5х = х - 5х = -4х
х −(−)2х =х+2х =3х
ДЕЙСТВИЕТО събиране или изваждане на подобни едночлени се нарича ПРИВИДЕНИЕ |
Задача 7.Извършете означените действия
А) 2х +(−)6х +х
Б) 3ах +5ах – 8ах
В)−2х2k−(−0,7х2k)−0,2х2k
Решение
А) Разкриваме скобите и получаваме :
2х +(−)6х +х =
2х −6х +х =
(2-6+1)х
=-3х
Б) 3ах +5ах – 8ах
= (3+5-8)ах
=0.ах
=0
В)−2х2k−(−0,7х2k)−0,2х2k
=−2х2k+0,7х2k−0,2х2k
=(-2 +0,7-0,2) х2k
=-1,5х2k
С привидение на подобни едночлени намираме неизвестно число в дадено равенство |
Задача 8 .Намерете неизвестното число
А) x + 9x = -80
Решение От x + 9x = -80, получаваме ,че 10.х=-80 с неизвестен множител х=-80:10 , х =-8
B) - 12x + x = 11
Решение
-12 x + x =11 .Тогава -11.х=11 , откъдето намираме,че х=11: (-11) , х=-1
C) х+0,5х+4,5х= 12
Решение След привидение на подобните едночлени х+0,5х+4,5х
,получаваме равенството ( 1 +0,5 + 4,5).х=12 с неизвестен множител х=12: 6 , х =2
Бележка :При действие привидение на подобни едночлени прилагаме дистрибутивното (разпределителното свойство) на действие умножение
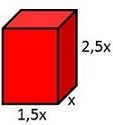
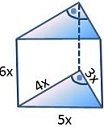
Задача 9.По данните на чертежа ,намери х ,ако сборът от всички ръбове на правоъгълния паралелепипед е 80 см
Решение Изразен чрез х ,сборът от всички ръбове на паралелепипеда е равен на :
4(1,5х)+ 4.х+4.(2,5х)
= 6х+4х+10х
= 20х
За х получаваме равенството 20х=80 ,от което намираме,че х= 4 см
Задача 10 .Ако разликата в обиколките на правоъгълника и триъгълника на чертежа е 16 см,то намерете х.
Решение
Обиколката на правоъгълника е 2(8х+4,5х)=2.12,5х=25х
Обиколката на триъгълника е 2.2,5х+4х=5х+4х=9х
От условието получаваме равенството 25х -9х= 16 ,от което намираме,че х=1 см
Задача 11 .Една тетрадка е три пъти по-скъпа от един химикал .За 2 тетрадки и 4 химикала ученик платил 20 лева .Намерете цената на една тетрадка ?
Решение :Нека цената на един химикал е x лева .
Тогава една тетрадка ще струва 3x лева .
От равенството 2.3x+4x=20 ,намираме,че 10x=20 лева, х=2 лева
Тогава тетрадката струва 2.3=6 лева
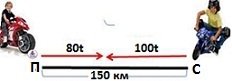
Задача 12 . Разтоянието между градовете София и Плевен е 150 км .Двама мотористи единият със скорост 80км/ч ,а другият със скорост 100 км/ч тръгват едновременно един срещу друг от двата града .Намерете в колко часа ще се срещнат мотористите ,ако те са тръгнали в 11 часа
Нека след t часа мотористите се срещнат.
Тогава мотористът със скорост 80 км/ч ще измине път равен на 80 t
,а мотористът със скорост 100 км/ч ще измине път равен на 100 t
Понеже пътуват един срещу друг ,то е вярно равенството 80 t+100 t=150
,откъдето намираме,че t =150/180= 5/6 часа ,което е 50 минути
Тогава двамата мотористи са се срещнали в 11 часа и 50 минути
Задача 13 . В един сладкиш захарта ,маята и брашното са в отношение 1:2:56 Ако общият грамаж на продуктите е 590 грама ,то намерете колко грама тежи всеки от продуктите .
Решение
Нека един дял от всеки продукт тежи х грама .Тогава 590 грама ще тежат 1х +2х +56х= 59х грама
От равенството 59х =590 ,намираме,че х=10 грама .Тогава брашното е 560 грама ,захарта 10 грама ,маята 20 грама .
1.5 Задачи за самостоятелна работа
Едночлен . Събиране и изваждане на подобни едночлени
1.задача :Запишете само тези изрази,които са едночлени
А)4а+3в;
Б)-3вс;
В) 2х - y2;
Г) 22аxy 2(с)3
2. задача : Намерете нормалният вид на едночлените и определете коефициентите им.
А) 8n3x .(- 2) x4 .0,5n4
Б) 7,4 х 5.z (− x 2z 2)
В) xy4z5x3z2y6
3.задача : Намерете степента на всеки от едночлените :
А) 72.x2 y3 z5 B) 62.x5y z4 C) 62.x4y2 z5 D) x6y4 z2
4.задача Кой от едночлените е от 10 –та степен
А) x y3 z5
B) x5y z4
C) 2.x4y2 z5
D) y4z2
5.задача :Приведете едночлена 0,5.x2 y3 z5 (- 2)3.x4y2 z5 в нормален вид и запишете неговият противоположен
6.задача :Намерете сбора на подобните едночлени :
А) 2x2 + x2 + 7x2
B) - 12х4 +1,5x4 + 2,5х4
C) -2а3x2 + 10,5х2а3
7.задача Намерете разликата на подобните едночлени
А)12асх6-17асх6;
Б) -5х2у3-12х2у3;
В) 1,2ух-2ух;
Г) 7авс3-9ас3в
8.задача:Опростете изразите
A)13 xy -28xy +19 xy
Б) -7x3y3x +25 x3y2x y - 18y3x4
9.Намерете неизвестното число
А) -х + 10x = 90
B) 12x -8x =- 12
C) 0,2х-1,2х+3,5х=8
10.Намерете неизвестното число
А) 1,2= 0,8x + x
Б) 2 = (0,5x - 1,5) + 1,6x
С) 4,3x - (0,8x + 1,6) = 5,8
Д) 4,1x + 2,7x : 3= 1,6
11. задача Дължините на страните на триъгълник са в отношение 3:5:4 .Намерете страните му,ако обиколката му е 144 см .
12.задача. От град А тръгнал моторист , движещ се със скорост 50 km/h. Два часа по-късно по същия път(от град A) след него тръгнал друг моторист със скорост 60 km/h. Намерете след колко време вторият турист ще настигне първия ?
2. Умножение , деление и степенуване на едночлени .
2.1 Умножение на едночлени
От предната точка ние събирахме и изваждахме само ПОДОБНИ едночлени.
Всеки два едночлена умножаваме като :
- умножим коефициентите им
- умножим степените с равни основи
Да разгледаме примерите:
Пример : (5х).(10y) =( 5.10)xy = 50xy
Пример : ( 1,5nm).(2mn ) = (1,5.2).n n m m=3n2m2
Пример : (7x2yz4).(0,6yz3x4)=(7.0,6) x2 x4y y z4z3 =4,2x4y2z7
ИЗВОД : След като умножим два едночлена получаваме едночлен приведен в нормален вид |
Задача 14 : Намерете произведението на едночлените 3x2y и 0,9 x5y5
Решение : (3x2y) . (0,9 x5y5) = (3.0,9) x2x5yy5 = 2,7 x7y6
Задача 15 :Намерете произведението на едночлените
А) x2y и 2xy5
Решение (x2y).(2xy5 )=2.( x2х).( yy5)=2x3y6
Б) 0,5abx2 и 20 a 3b4x
Решение (0,5abx2).(20a3b4x )= 0,5.20aa3 bb4x2x =10a4b5x3
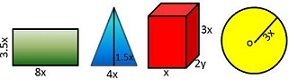
Задача 16 :По данните на чертежа съставете израз , с който да намерите :
- лицето на правоъгълника,триъгълника и окръжността
- обемът на правоъгълната призма
Решение
Лицето на правоъгълника е : ( 3,5х) .(8х)=28х2
Задача 17. На чертежа е дадена е права триъгълна призма с основа правоъгълен триъгълник с катети равни на 3х см и 4х см и хипотенуза 5х см .Ако височината на призмата е 6х см ,то съставете изрази ,за :
А) лицето на основата В
Б) околната повърхнина S
B) пълната повърхнина S1
Решение
А) В=(4х.3х):2=12х2:2 = 6х2
Б) S=6х.(4х+3х+5х) =6х.12х=72х2
В) S1= 2В + S =2.6х2 + 72х2=84х2
2.2 Степенуване на едночлен
ПРАВИЛО : Едночлен степенуваме ,като степенуваме всеки негов множител |
Пример : (5хy)2 = 52x2y2= 25x2y2
Пример : (-2n3m4)3 = (-2)3 .(n 3 ) 3 (m 4) 3 = -8n9m12
Пример:
1
Задача 18 . Степенувайте едночлена (54х3y2 0,24yх)3 и намерете числената му стойност за x=2 и y=-1.
Решение
Извършваме означените действия и получаваме :
(54х3y20,24yх)3
={ (5.0,2)4 х4.y3}3
= х12y9
За х=2,y=-1 , числената стойност на израза e : - 212 =- 4096
Задача 19.Степенувайте едночлена (3а3b3ba)2 и намерете неговата числена стойност за а= -4, b=0,5 ,
Решение
Привеждаме основата на едночлена в нормален вид и получаваме (3а4b4)2= 32а6b6
Понеже аb= -4.0,5 = -2 ,то в този случай представяме едночлена,като степен на произведението аb
32а6b6 = 9.(ab)6
Тогава числената стойност на израза (3а3b3ba)3 за а= -4, b=0,5, е 9.(-2)6 = 576