Интересни задачи от домино,зарове и стрелички.
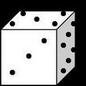
Задача За всяко от двете зарчета на фигурата е намерен сборът от точките върху невидимите стени.
Сборът от броя на точките върху срещуположните стени на всяко зарче е седем.
Да се намери разликата на тези две числа
А) 7 Б) 8 В) 13 Г) 11 Д) 6
(МГ”Баба Тонка”-гр.Русе ,прием след 4 клас)
|
Задача Симеон направил фигура с помощта на 7 правоъгълни плочки от вида:
Той поставил една до друга плочките така, че да се допират страни с еднакви числа.
Сборът от числата на получената фигура е равен на 33 (виж картинката). Кое число е било на мястото, означено с въпросителен знак,ако всички числа са естествени или числото нула ?
A) 2 B) 3 C) 4 D) 5 E) 6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 | 2 |
|
| ? |
| 1 | 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| 1 | 0 | 0 | 5 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
Да потърсим сбора на всички известни от условието на задачата числа.
Той е : 1+0+0+5+5+3+3+2+2+1+1+2=25
От това,че
- 33 -25 =8
- Две еднакви числа се допират
- Правим извода,че търсеното число е 4
|
Задача Колко различни резултата могат да се получат с помощта на две стрели и показаната мишена?
Пример :Ако стрелите са с попадения в мишени с 2 и 3 точки то,резултатът е 5 точки .
(Международно състезание „Европейско кенгуру”)
2 |
|
|
|
|
| 3 |
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение.
Под различен резултат ще разбираме различен
сбор от точките получени при хвърляния на две
стрели .Попаденията 2 и 3 или 3 и 2 ще броим
за един резултат.
Възможностите са :
- 2+2=4
- 3+3=6
- 6+6=12
- 2+3=5
- 2+6=8
- 3+6=9
|
Задача Симеон направил фигура с помощта на 7 правоъгълни плочки от вида
Той поставил една до друга плочките така, че да се допират страни с еднакви числа.Числата са естествени или числото нула.
Сборът от числата на получената фигура е равен на 39 (виж картинката). Кои числа са били на мястото, означено с въпросителни знаци?Опишете всички възможни числа?По колко различни начина може да се подреди доминото ?
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| 3 | 2 |
| ? | ? |
| 1 | 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| 1 | ? | ? | 5 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упътване.Ако числата които търсим имат сбор, примерно 6,то всички възможни начини за това са : 6= 1+5 = 2+4 = 3+3 = 0+6 , четири двойки възможни числа . Всяка двойка числа може да си разменя местата при подреждане на доминото
.
|
Задача Слагаме три зара един върху друг , за да направим кула ,но го правим така,че стените които се допират ,да имат еднакви числа.Една от кулите която посочваме тук ,може да се направи ,другата не . Известно е ,че сборът от точките върху всеки две срещуположни стени на зарчето е 7.
Коя е невъзможна за постигане кула?
Решение От условието всички срещуположни стени имат сума 7 следва,че противоположните стени на зара са :
1 и 6 или 2 и 5 или 3 и 4.Това са и всички възможности за получаване на сума 7 от числата 1,2,3,4,5 и 6 .
Следователно ако допираме едно с едно ,то ще трябва да допираме и шест с шест .Разглеждаме всички случаи на образуване на кулите по това правило.
- Нека нареждаме едно с едно ,съответно шест с шест .Не е възможно да построим втората кула защото ,тя има страничен зар единица.(В този случай и трите единици и шестици са долепени едни върху други)
- Нека долепяме 2 с 2 ,съответно 5 с 5.Не можем да построим нито една от кулите.
- Нека долепяме 3 с 3 , съответно 4 с 4.Отново няма да можем да построим нито
една от кулите .
Показахме ,че от всички възможни случаи на долепване е възможно да построим само първата кула.Невъзможна за построяване във всички случаи е втората кула .
|
Задача.На чертежа са дадени три зарчета залепени едно над друго .Сборът от точките на всеки две залепени стени е 5.На предната стена на долното зарче има една точка. Останалите стени са замацани и точките не се виждат.Колко са точките на горната стена на най-горното зарче ,означено с Х, ако сборът от точките на всеки две срещуположни стени на всяко от зарчетата е 7? (без залепените)
А)2 В)3 С)4 D)5 Е)6
(МАТЕМАТИЧЕСКО СЪСТЕЗАНИЕ "ЕВРОПЕЙСКО КЕНГУРУ")
Решение От това,че всички незалепени стени на зарчетата имат сума 7 ,то срещу едно на първия зар стои цифрата 6. От останалите стени на първото зарче 2,3,4 и 5 ,сума 7 можем да образуваме по два начина 2+5 или 3+4 .
Нека другите две незалепени стени са 2 и 5.Тогава залепената стена на първото квадратче е 3 или 4 .Ако първата залепена стена е 3 ,то тя е залепена с 2 ,тя е залепена с три и така нататък.
В този случай ще получим четири стени които имат точки 2 ,което е невъзможно.
Аналогични са разсъжденията ,ако първата залепена стена е 4.Ще ни трябват четири единици ,което е невъзможно.
Остава възможността страничните стени да са 3 и 4.
Точно една е възможността за залепената стена на първото зарче и тя е 2.
Тогава на мястото на Х ще стои стена с 2 точки.
|
Задача . Стрелец изстрелял три стрели по мишената, показана на
чертежа. Той уцелил при трите изстрела и получил съответни точки
съгласно показаните числа в различните мишени. Колко различни
резултата могат да се получат след сумиране на точките?
A) 13 B) 17 C) 19 D) 20 E) 21
(Математическо състезание „Европейско кенгуру”)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 | 3 | 7 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упътване Разгледайте всички възможни попадения и съответните сборове
ЗадачаРалица направила четири еднакви кубчета с номерирани стени..Стените на всички кубчета са номеририни ,като двойки с номера (1,2),(6,4) и (3,5),като всяка двойка са срещуположни стени .
След това тя ги залепила така,че да получи правоъгълен паралелепипед с измерения 4 cm,4cm,1cm , като залепвала само стени с еднакви номера .Накрая Ралица събрала числата по повърхността на получения паралелепипед .Кой е максималният сбор ,който може да получи тя?
A) 66 B) 68 C)72 D) 74 E)76
(Математическо състезание „Европейско кенгуру“)
Решение
Стените на всички кубчета са номеририни ,като двойки с номера (1,2),(6,4) и (3,5)
За да получи Ралица максимална сума ,то тя трябва да залепи кубчетата , по стените които са номерирани с най-малките числа .
Нека залепи двойка кубчета със стените номерирани с единица .Тогава числото две е записоно в срещуположната стена . За да получи най -голям сбор е необходимо и другата двойка от кубчета да са залепени със стени номерирани с единица .
При залепването на двете двойки залепени кубчета ,за да получи максимална сума , Ралица трябва да залепва стени номерирани с числото три. По този начин на залепване тя ще получи максимална сума и тя е :
4(1+2+3+4+5+6) - 4.1+4.3 = (4.6.7):2 -16=84-16= 68
|
Задача Тяло е получено чрез залепване на три еднакви зара едно над друго ,така ,че всеки две залепени стени са с еднакъв брой точки .
Известно е ,че сборът от точките върху всеки две срещуположни стени на заровете е 7 . Кое от посочените по долу тела е получено по този начин ?
Телата са погледнати отстрани.
( международно състезание „Европейско Кенгуру”2011),
A) 1 B)2 C) 3 D) 4 E) 5
|
Задача На стените на куб са написани числата 3,4,5,6,7 и 8 Кубчето е хвърлено 2 пъти. Първият път сборът от числата на страничните стени е 20,а вторият път сборът от числата на страничните стени е 25.Кое число е написано на стената, която лежи срещу стената ,на която е написано числото 6?
(Математическо състезание Академик „Кирил Попов” ,Шумен ,Отборно състезание)
Решение Знаем сборът от четирите странични стени,следователно можем да определим сборът на останалите две стени, на едната от които е паднал кубът.
За първото хвърляне (3+4+5+6+7+8)- 20=13
За второто хвърляне (3+4+5+6+7+8) - 25=8
Сбор 13 от две числа можем да получим по следните начини 13=6+7=5+8
Сбор 8 =3+5
Следователно само при първото хвърляне получаваме точно един случай в който една от стените е 6 .Търсеното число е 7 .