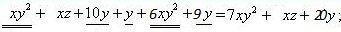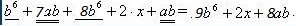Правилна четириъгълна призма  с основен ръб  а см  и височина h  има обем 9 пъти по –малък  от  друга правилна четириъгълна призма  с основен ръб равен на  основният ръб  на  първата призма .Съставете  израз  за сбора от обемите на двете призми ,в който да участват  само а и h .

Решение

Обемът на призмата с  основен ръб а см и височина  h  е  равен на  V  =В.h ,където В=а²

Обемът на призмата V₁ с височина h₁   е равен на  V₁ =  В.h₁ , където В=а²

От това,че   V₁ =  9V  получаваме равенството  В.h₁ =  9В.h    ,от  което  намираме,че    h₁ =9h  

Тогава изразът , който  е сбор от обемите на двете призми   е   а² h   + 9а² h = 10а² h  

Този  израз е сбор от подобни   едночлени .

Решенията на много задачи от   практиката  и науката  са  изрази ,които са  сбор от едночлени ,затова  те се изучават  в отделна  математическа дисциплина  наречена   алгебра .

Примери   за многочлени   : -4x ; 5x +1  ;   3x³-3x²-5xy +x³ ;   yx³ – x² –yx³ +1 ;  z²x  – z⁴

• ВСЕКИ ОТ    ЕДНОЧЛЕНИТЕ е  приведен в нормален вид   

• МЕЖДУ  ЕДНОЧЛЕНИТЕ няма   подобни едночлени

Примери за многочлени приведени в нормален вид :

• 5x + 4y -6

• 3x³-3y²-5y  - x

• 4z²  -3z⁴ +x³ -2

• x⁴ + x³ – x² – x +1

Примери за многочлени , които  не са  приведени  в   нормален вид :

•   x - 4x –1

• 3y²-5yy  - x²

•   z²  -3z⁴ +z⁴ -2

• x⁴ + x³ – 2x³ – х²x² +1

1.задача .Приведете   многочленът   xy²  +xz +10y+y+6xy²+9y  в нормален вид .Намерете  неговите коефициенти  и  определете  неговата степен.

Решение

 ПОДЧЕРТАВАМЕ  ПОДОБНИТЕ ЕДНОЧЛЕНИ   С РАЗЛИЧНИ  ЧЕРТИ

 СЪБИРАМЕ ИЛИ ИЗВАЖДАМЕ   ПОДОБНИТЕ ЕДНОЧЛЕНИ   

От нормалният вид на многочлена  7xy² + xz +  20y, намираме,че  неговите  коефициенти са  - 7; 1 ; 20 .Даденият многочлен е от   3-та  степен (едночлена с най-висока степен е  7xy² )

Той  има    коефициенти  - 9; 2 ; 8    и  е от степен 6-та

3.Задача Приведете многочлените в нормален вид  .

а) 2,5 .4х  + 9х +1 ;

б)  5х⁵ +3х² – х⁵ + 2х² – 6х +х - 2

в) 0,9х⁵ +3х² – х⁵ + 2х² + 4х – х

4.задача Приведете многочлените в нормален вид и намерете числената им стойност за  x= 3 , y = -2

а) х⁵ +4y² – х⁵– 3y² – 2х +х – 2y

б) 0,2 х³- 9y²  –  х³ + 10y² + 0,8х³ – х

5.задача Приведете многочлените в нормален вид и намерете числената им стойност за  а= 2 , b= -0,5

а) 2а⁵b⁵   -  аb(-5а⁴b⁴) +  4а³ + а³;

б)-2a²b.(-3ab²) - 6a³b³+ 30b²   -70b²;

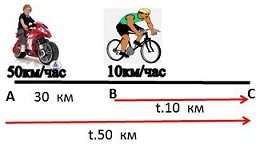
6.задача.На  чертежа   са дадени градовете A и B  разтоянието , между които е 30 км .В  11 часа  едновременно  от град А тръгнал моторист ,а от град В  в  същата  посока  велосипедист.Мотористът  пътувал със скорост  50 км/ч  , а велосипедистът   със скорост  10 км/ч  . Намерете в колко часа  мотористът  ще настигне  велосипедистът ?

Решение

Нека  след   t  часа  мотористът  и  велосипедистът  се срещнат  в  точка С .

Тогава велосипедистът е изминал път равен на 10.t ,а  мотористът  път равен на 50 t

Тогава разтоянието   50 t  -  10 t    е    точно 30 км .

От равенството    50 t  -  10 t =30  ,намираме,че  t = 3:4=45 минути

Тогава  мотористът е настигнал велосипедистът точно в  11часа и  45 минути

Пример :  Дадени са многочлените 

f=5x +1  , q=3x³-3x²-5x  и  g = x³ – x² – x +1

А)Намерете  нормалният вид  на  многочлена   f  + q  +  g

Б) Намерете  нормалният вид  на  многочлена   f  + q  -  g

Решение

А)   f  + q  +  g  = 5x +1  +3x³  -  3x²  -  5x + x³ – x² – x +1

=4x³ – 4x² – x + 2

Б)   f  + q  -  g  = 5x +1 + 3x³-3x²-5x  - ( x³ – x² – x +1)

=5x +1  +3x³  -  3x²  -  5x - x³ + x² + x -1

=2x³ – 2x² – x

7.задача  Дадени са многочлените 

f=2x² -х+1  , q=3x+1  и  g =  – x² – x -1

А)   Намерете  нормалният вид на многочлена  f  - q  +  g

Б)  Намерете  нормалният вид на многочлена  f  + q  -  g

8.задача.Разкрийте скобите и направете   приведение на подобните едночлени

А)  6y⁵ +3y⁴ + 4y³ +y +1  -( 2y⁷ +3y⁴ + y³ +5y +1 )

Б)  х⁵ -(3y⁴ + х⁵ +y +3)+  х  - ( 2х⁷ - 7y⁴ + 2y  +5х +1 )

9.задача.Покажете,че числената стойност на израза А= 5х⁵ –(х⁵+ 2х³  +х +6) -( 4х² х³ -2 х³ -х +7 ) не зависи от х

Решение

Разкриваме скобите ,унищожаваме противоположните едночлени  и правим привидение на подобните едночлени

А=   5х⁵ –(х⁵+ 2х³  +х +6)  -  ( 4х²х³ -2х³ -х +7 )

А=   5х⁵ –х⁵- 2х³  -х - 6 - 4х⁵+2х³ +  х - 7

А= - 6-7=  -13

Тогава А  не зависи от променливата  х .

10.задача.Разкрийте скобите , направете   приведение  и покажете,че числената стойност на израза не зависи от х .

А)  х⁵ +3х⁴+ 2х³  +х +1  -( х²х³+2.1,5х⁴ +2х³ +х +7 )

Б)  а³х³ - y³ -( ах)³ + 2.х² х⁵  - ( 2х⁷ - y³ + a +1 )

11.задача Съставете израз ,който е сбор на три последователни естествени числа

Решение

Нека най-малкото число е х ,тогава  числото след  него е  х+1 .

Тогава числото след х+1 е х+2  

Тогава търсеният израз е :х+х+1+х+2=3х+3 

12.задача Съставете израз ,който е сбор на три последователни  четни  естествени числа

Упътване : Означете първото число с 2х

Отговор 6х+6

13.задача Намерете  четири последователни естествени числа със сбор   34 .  

Решение

Числата са х ,х+1,х+2,х+3   и имат сбор  х +х+1+х+2+х+3=4х+6 

От равенството  4х+6  =34  ,намираме,че 4х=28   и х= 7

Тогава числата са 7,8,9  и 10

14.задача Намерете   три   последователни  нечетни  естествени числа със сбор   69 .  

15.задача Опростете израза   M  = 10⁴ (х³y²0,5 )⁴– 624 х¹²y⁸ +  0,5xy +1   

 и  намерете   числената  му  стойност за   x= -2 и  y=1.

 Отговор 2¹² =4096

16.задача  Даден е   изразът    А  =  х⁵ – (-2x² +x⁵ ) + 1  . Покажете,че за  всяка стойност на променливата х, изразът А  приема само  положителни  стойности .

Решение Опростяваме изразът и получаваме  А  =  х⁵ + 2x² –x⁵  + 1 = 2x²  + 1   

За всяка стойност на променливата х,числото  2х²  > 0  ( по-голямо или равно на нула )            

Тогава  изразът  А  =  2х ²  + 1 > 0  (по-голямо от нула )

17.задача  Даден е   изразът    N  =  2x³ – 2x² – x  -  (2x³ – x  ) -5    

А) покажете,че за  всяка стойност на променливата х  , изразът N  приема само отрицателни стойности .

Б)  Намерете за кои стойности  на х ,изразът   N  приема   най-голяма стойност

Решение

А)   N  =  2x³–2x²–x -2x³ +x -5= -2х² -5    

 За всяка стойност на променливата х ,числото -2х²  е  отрицателно  или нула .

Тогава  изразът   N  = - 2х² -5  < 0

Една примерна таблица за числената  стойност на N за избрани стойности на  х .

  Б)   Числената стойност на  многочленът   N  = - 2х² -5  < 0  ще е най-голяма за х =0 , защото за всички други значения на х , N ще има числена стойност   по –малка  от  (-5)   .

18.задача  Даден е   изразът    N  =  2x⁴ + 2x² – x  -  (2x⁴ – x  -7)    

А) покажете,че за  всяка стойност на променливата х  , изразът N  приема само положителни  стойности .

Б)  Намерете за кои стойности  на х ,изразът   N  приема   най-малка   стойност