Общо кратно. Най-малко общо кратно .5 клас
Съдържание :
1.Кратно .Общо кратно
2.Най-малко общо кратно
2.1 Най-малко общо кратно на две числа
2.2 Тест - проверка на уменията за намиране на НОК на две числа
2.3 Най-малко общо кратно на три числа
3.Практически задачи
1.Кратно .Общо кратно
Кратно число — това е естествено число, което се дели на друго естествено число без остатък.
Примери :
- Числото 18 е кратно на 9 (18:9=2)
- Числото 45 е кратно на 5 (45:5=9)
- Числото 30 е кратно на 2 (30:2=15)
Да разгледаме числото 9
Делителите на числото 9 са числата 1,3 и 9 .Те са краен брой .
Числата 9,54,36 и 81 са кратни на числото 9 .Има безбройно много числа ,кратни на числото 9 .
Всички кратни на числото 9 ,можем да подредим в редица ,като започнем от най-малкото .
Записваме : К(9) = {9, 2.9, 3.9, 4.9, 5.9 ,........}= {9,18,27,36,45 ,......}
Всички кратни на естественото число а,съкратено записваме К(а )
Задача за упражнение .Запишете следващите две кратни на числото 9:
К(9) = {9, 18,27, 36, 45 , (..),(..)......}
Задача за упражнение.
А) Запишете всички делители на числото 6
Д (6) = {......}
Б) Запишете пропуснатите кратни на числото 6 :
К (6) = {6,12,18, (....), 30 ,(...),......}
Да запомним!
Числата ,които се делят на дадено естествено число без остатък са безбройно много
Кратните на простото число 7 са : К (7) = { 7: 14, 21, 28, 35 .....}
Делителите на простото число 7 са : Д (7) = { 1, 7 }
Общо кратно на две естествени числа е такова естествено число, което се дели и на двете числа без остатък
Пример :
Числото 2 се дели без остатък на 12 и числото 3 се дели без остатък на 12
Тогава естественото число 12 е общо кратно на числата 2 и 3
Вижте как костенурката Многознайка е получила всички общи кратни на числата 2 и 3
Общите кратни на числата 2 и 3 са безбройно много
Най-малкото от всички общи кратни е 6
Записваме : ОК (2, 3)= { 6, 12 , 18, 24 ..........}
Пример : Запишете всички общи кратни на числата 2 и 5
Всички кратни на числото 2 са :
К (2) = {2,4,6, 8, 10 , 12,14 ,16,18,20,22 , ......}
Всички кратни на числото 5 са :
К (5) = { 5,10,15, 20, 25 , 30,35 ......}
Всички кратни на 2 и 5 са : 10, 2.10 , 3.10,4.10 .........................
Тогава ОК( 2,5) = { 10, 20 , 30,40 ..........}
Най-малкото от всички естествени числа,които се делят без остатък на 2 и 5 е числото 10
2.Най-малко общо кратно
2.1 Най-малко общо кратно на две естествени числа
Определение :
Най-малкото общо кратно на две числа – това е най-малкото естествено число , което дели и двете числа без остатък
Най-малкото общо кратно на естествените числа а и b се означава с НОК (а, b)
Първи начин за намиране на НОК на две естествени числа
Записваме в редица всички кратни и на двете числа ,докато открием първото число ,кратно и на двете числа
Пример. Намерете най-малкото общо кратно на числата 6 и 9
К (6) = { 6, 12, 18, 24, 30,36 ...}
К (9) = {9, 18, 27, 36, ...}
НОК (6, 9) = 18
Пример : Намерете най-малкото общо кратно на числата 12 и 18
К (12) = {12,24,36,48,60,72 .......}
К (18) = {18,36,54,,72 ..........}
НОК (12, 18) = 36
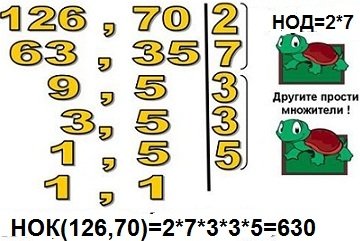
Втори начин : Намиране на НОК ,чрез разлагане на прости множители
За да намерим НОК,първо трябва да намерим общите прости множители на двете числа
Да си припомним !
Най-големият общ делител на две числа е най-голямото естествено число,на което се делят и двете числа
- Записвам числата едно след друго хоризонтално и след последното число тегля черта.
- Започвам делението с общите прости множители
- Започвам с най-малкото просто число- общ делител на двете числа .Делителят записвам в дясно.
- Деля всички числа с него, а получените частни записвам под дадените числа.
- Числата, които не се делят на общия прост множител , преписвам на втория ред.
- С числата от втория ред постъпвам по същия начин.
- Като приключа с общите прости делители ,продължавам с делителите на всяко от числата
- Делението продължавам, докато в ляво от чертата от всяко число получа частно единица.
- Умножавам получените прости делители в дясно от чертата и получавам НОК на дадените числа.
Как да намерим НОК ,ако числата нямат общи делители
Ако естествените числа а и b са взаимно прости ,то НОК (а , b)= а * b
Това е така,защото произведението а * b е най-малкото естествено число ,което се дели и на двете числа без остатък
Пример : НОК( 3, 7) =21
Пример : НОК( 5, 71) =355
Пример : НОК( 3 , 200 ) =600
Задача за упражнение . Намерете НОК на числата
А) 8 и 9
Б) 18 и 5
В) 500 и 2
Колко е НОК ,ако едното число се дели на другото ?
Пример : НОК(300,6300 )= 6300, защото 6300 се дели на 300
Продължаваме с намирането на НОК на две числа в случаите ,когато имат общи делители
| 105 | ,90 | 3 | 360 | ,80 | 2 | |||
| 35 | ,30 | 5 | 180 | ,40 | 2 | |||
| 7 | ,6 | 7 | 90 | ,20 | 2 | |||
| 1 | ,6 | 2 | 45 | ,10 | 5 | |||
| ,3 | 3 | 9 | ,2 | 2 | ||||
| ,1 | 9 | ,1 | 3 | |||||
| 3 | 3 | |||||||
| 1 |
| 65 | ,90 | 5 | 250 | ,80 | 2 | |||
Извод :
Щом общите прости множители се умножават, при намиране на НОК , можем спокойно да делим на произволни общи делители
| 150 | ,90 | 30 | 560 | ,160 | 80 | |||
| 5 | 3 | 5 | 7 | 2 | 2 | |||
| 1 | 3 | 3 | 7 | 1 | 7 | |||
| 1 | 1 | |||||||
2.2 Тест - проверка на уменията за намиране на НОК на две числа
Задача №1.Най-малкото общо кратно на 4 и 5 е :
А) 4 Б) 5 В) 20 Г)10
Задача №2.Най-малкото общо кратно на 8 и 9 е:
А) 9 Б) 18 В) 16 Г)72
Задача №3.Най-малкото общо кратно на 4 и 16 е :
А) 4 Б) 16 В)8 Г) 12
Задача №4.Най-малкото общо кратно на 10 и 40 е :
А) 10 Б) 20 В) 40 Г)80
Задача №5. Най-малкото общо кратно на 8 и 12 е :
А) 12 Б)36 В) 24 Г)8
Задача №6. Най-малкото общо кратно на 70 и 15 е :
А) 10 Б) 140 В)70 Г)210
Задача №7. Най-малкото общо кратно на 80 и 120 е :
А) 160 Б) 240 В) 120 Г)180
Отговори :
Задача | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Отговор | В | Г | Б | В | В | Г | Б |
Лесно и бързо се намира НОК чрез НОД
НОД е произведение от всички общи прости делители на двете числа
Правило :
За да получим НОК от НОД го умножаваме с останалите прости множители
С признаците за делимост , можем бързо и лесно да намерим НОК
Задача : Колко е НОК (725; 400).=?
Решение
От признаците за делимост,виждаме ,че и двете числа се делят на 25
На 25 се делят числата ,които завършват на две нули или на 25,50 или 75
725=25* 29
400=25 *16
Тъй като (29,16)=1, то НОД(725; 400 ) =25
Тогава НОК (725; 400)= 25* (29* 16) = 11600
Задача .Намерете НОК( 360 , 585)= ?
Решение
От признаците за делимост,виждаме ,че и двете числа се делят на 9 и 5 .
Тъй като ОД (9,5)=1 , то двете числа се делят на 45
Тогава 45 е общ делител на двете числа
360=45* 8
585=45*13
Тъй като (8,13)=1 , то НОД (360 ,585 ) =45
Тогава НОК (360; 585)= 45* (8* 13) = 4680
Когато числата са по –големи ,ползваме програми за намиране на НОК
2.3 Намиране на най-малко общо кратно на повече от две числа
| 24 | 18 | 60 | 6 | 72 | 30 | 75 | 3 | |||
| 4 | 3 | 10 | 2 | 24 | 10 | 25 | 5 | |||
| 2 | 3 | 5 | 2 | 24 | 2 | 5 | 2 | |||
| 1 | 3 | 5 | 3 | 12 | 1 | 5 | 5 | |||
| 1 | 5 | 5 | 12 | 1 | 12 | |||||
| 1 | 1 | |||||||||
| 45 | 105 | 60 | 15 | 540 | 360 | 90 | 10 | |||
| 3 | 7 | 4 | 3 | 54 | 36 | 9 | 9 | |||
| 1 | 7 | 4 | 4 | 6 | 4 | 1 | 2 | |||
| 1 | 7 | 1 | 7 | 3 | 2 | 2 | ||||
| 1 | 3 | 1 | 3 | |||||||
| 1 |
| 15 | 10 | 20 | 400 | 360 | 70 | |||||
3.Практически задачи
Задача за упражнение.На спирка пристигат едновременно три автобуса . След колко време тези три превозни средства отново ще се срещнат на тази спирка, ако по график първият прави пълна обиколка на маршрута си за 1 час и 30 минути , вторият - за 1 час, а третият за 45 минути ?
Упътване :Намерете НОК(90,60,45)
Отговор :след 180 минути=3 часа
Задача за упражнение Възрастта на моята баба е равна на най-малкото естествено число,което се дели без остатък едновременно на числата 2, 3,6 и 11 . На колко години е моята баба ?
Отговор :НОК( 2, 3,6 , 11)=66 години
Задача за упражнение Броя на учениците в един клас се дели на 5 и 6 .Ако те са по-малко от 35 ,то намерете броя на учениците в този клас
Отговор : 30
Често в задачи от практиката се добавя и уточняване на дата от месеца
Задача Днес 1 април приятелите Петър и Стоян тренират заедно плуване .Ако Стоян ходи на тренировки на всеки 3 дни,а Петър на всеки 4 дни ,то коя е най-близката дата ,на която те отново заедно ще тренират плуване ?
Решение
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стоян |
|
|
|
|
|
|
|
| |||||
Петър |
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
НОК(3,4)=12
Тогава на всеки 12 дни след първия път когато са тренирали заедно ,те отново ще тренират заедно
Тогава точно на 13 април ,те ще са заедно на тренировка
Задача за упражнение Днес 3 декември Мая и Петър са заедно на урок по математика.Ако Мая ходи на уроци на всеки 4 дни,а Петър на всеки 5 дни ,то коя е най-близката дата ,на която те отново заедно ще бъдат на урок по математика ?
Отговор : 24 декември
Понякога в задачи от практиката се иска освен уточняване на датата ,да уточним и в кой ден от седмицата се случва това .
Какво трябва да знаем
Всяка седмица има 7 дни
През всеки 7 дни ,дните от седмицата се повтарят
Ако днес 3-ти е вторник ,то на 3+7 ,3+2.7 ,....е отново вторник
Ще завършим с една такава изследователска задача за ученици с математически наклонности
Задача На всеки 4 дни ,мама почива два дни ,а на всеки 3 дни татко почива един ден .Днес 1 септември ,ден неделя е втория ден от почивката на мама .На този ден и татко не е на работа .
А) След колко дни мама и татко ще почиват за първи път отново заедно и в кой ден от седмицата ?
Б) След колко дни мама и татко за първи път ще почиват отново в неделя .Намерете месеца и датата
Решение
А) 1 септември е вторият ден от почивката на мама и ден в който и татко почива
| нед | пон | вт | ср | чет | пет | съб | нед | пон | вт | ср | чет | пет |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
мама |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Татко |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|