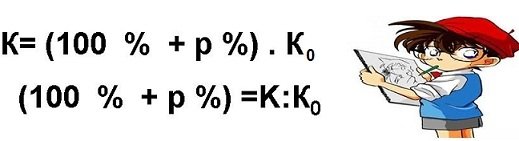За да съществуват  банките ползват   чужди парични средства за определено време

За времето,през което банките ползват чужди парични средства ,те изплащат възнаграждение ,което се нарича лихва

Първоначалната сума  вложена  от дадено лице  в банка  се нарича    начален капитал (депозит)

Времето ,за което се предоставя сумата се нарича  лихвен период 

В  края на всеки такъв    лихвен период  лихвата става платима.

Лихвата се изчислява,като процент от началния капитал

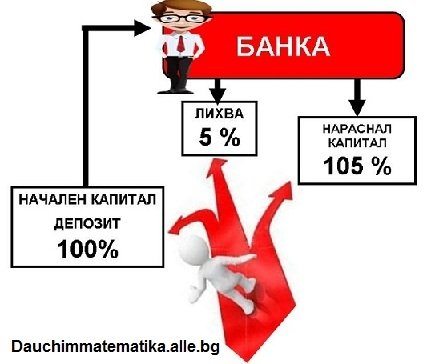
На схемата е показано ,как  в проценти  се формира нарасналия капитал

Банковото дело е сложна наука .Тя се занимава с лихва и капитал .

За да положим началото ,ще въведем означения и  ще  ползваме  формули  ,общи за всички задачи  свързани с изчисляване на лихва и нараснал капитал

 K₀ – начален капитал,

 р%   – лихвен  процент  за определен  период от време

L - лихва за  определен  период от време

K – нарасналият капитал в края на периода.

В  таблицата  ,е показано как   банките  днес  обявяват лихвените си проценти

Според таблицата , лихвените  проценти за съответните лихвени периоди са следните :

3 месеца   ,при  годишна лихва  0,24% .Тогава месечната  е 0,24 :12 =0,02%, а тримесечната - 0,06%

6 месеца   ,годишна лихва  0,27% .Тогава месечната  е 0,27 :12 =0,0225%, а тримесечната - 0,0675%

12 месеца   ,годишна лихва  0,36% .Тогава месечната  е 0,36 :12 =0,03% ,а тримесечната - 0,09%

                        p           
L= р % . К₀ =  — .  К₀   
                        100               

Задача .Пресметнете лихвата ,по дадени :

а) Начален капитал  К₀=20 000 ,лихвен процент  за  тримесечен  лихвен период р%=1,25%

Решение

L = 0,0125 .  20 000 =  250 лв    

б) Начален капитал  К₀=100 000 ,лихвен процент  за  шестмесечен   лихвен период р%=1,30%

Решение

L = 0,013 .  20 000 =  260 лв    

в) Начален капитал  К₀=50 000 , годишен  лихвен процент  1,2% за  шестмесечен   лихвен период

Решение

Щом лихвения процент е  годишен ,то шестмесечния е р%=1,2% :2=0,6 %

L = 0,006 .  50 000 =  300 лв    

Задача за упражнение  : Пресметнете лихвата ,по дадени

а) Начален капитал  К₀=45 000 ,годишен лихвен процент    р%=2% за едногодишен лихвен период

Отговор :   450 лв    

б) Начален капитал  К₀=150 000 , годишен  лихвен процент 2,4 % , за  шестмесечен   лихвен период

Отговор :  1800 лв   

К= (100  %  + р %) . К₀

Задача .Намерете натрупания  капитал по данните в таблицата 

Задача за упражнение .Намерете натрупания  капитал по данните в таблицата

Задача : Ако  внесете  депозит от   50  000 лв  ,с  договорена годишна лихва 5 % при 12 месечен лихвен период ,то намерете :

А)платимата  лихва

Б)  сумата , която ще получите в края на периода

Решение

А) Търсим  лихвата   L ,така е  сумата , която ни показва с колко е нараснал капиталът  ни за една година

 L = p% . k₀ =5 % . 50000=0,05.50000=2500 лв

Б) Търсим  k ( нарасналия капитал)

Задача : Фирма внесла в банка депозит  от  50  000 лв  при  договорената годишна лихва е   6 % , за тримесечен лихвен период . Намерете :

А)платимата  лихва за един лихвен период

Б)  сумата , която ще получите в края на този лихвен  период

Задача .Фирма  внесла в банка депозит от 40 000 лева  за 12 месеца .В края на периода  банката и изплатила  45 000 лева .Намерете   лихвения процент на банката за този период ?

Решение

Първи начин

Лихвата е 45 000 -40 000 = 5000 лв
               p           
L      =    — .  К₀   
              100               

               p           
5000=    — .  40 000   
              100               

Р :100 = 5000 :40000=0,125

Р =12, 5 %

Втори начин

Тогава   (100    + р ) % = 45 000 :40 000  = 1,125

   р%  = 0,125 = 12,5 %

К= (100  %  + р %) . К₀

 К₀ = К : (100  %  + р %)

Задача . Клиент внася в банка депозит с годишна лихва 4% за 12 месечен лихвен период.Ако в края на периода банката му изплати 8450 лева ,то намерете колко е бил депозита(началния капитал) на клиента .

Решение :

К₀ = К : (100  %  + р %)

К₀ =8450 : (100  %  + 4%)

К₀ =8450 : 1,04

К₀ =8450 : 1,04 =8125 лв

Задача  за упражнение   Клиент внася в банка депозит с годишна лихва 3 % за 12 месечен лихвен период.Ако в края на периода банката му изплати 30900  лева ,то намерете колко е бил депозита на клиента

Отговор 30 000  лева

Задача  за упражнение  Семейство внесло  на срочен влог определена сума, която в края на срока достигна  57680 евро при лихва 3%. Намерете сумата в евро  , която е внесена от това семейство .

Отговор :56000

Задача  за упражнение   Клиент внася в банка депозит с годишна лихва 6 % за 3 месечен лихвен период.Ако в края на лихвения  период  банката му е  изплатила   71050  лева ,то намерете колко е бил депозита на клиента.

Отговор 70 000  лева

Проста  лихва е лихвата, която се пресмята само върху началния капитал  

При олихвяването лихвата НЕ се прибавя към основната сума, за да носи и тя лихва през следващите периоди.

Сложна (капитализирана ) лихва е лихвата, която се  изчислява ,като към основния капитал се прибави лихвата от предходния период и в следващия период има лихва върху новата нараснала сума.

Когато даден лихвен период се повтори ,то  лихвата се капитализира

В повечето случаи , лихвата за втория лихвен период , се изчислява  ,със същия лихвен  процент 

Забележка : Повтарянето на периодите става с предварително договаряне с банките

Задача Дядото на Петър ,внесъл  депозит  от 12000 лв  за една година ,при лихвен процент 3,5% .Колко лева ще получи дядото :

А) в края на първият период (олихвяването е с проста лихва )

Б) в края на вторият период (олихвяването е със сложна лихва )

Решение

А) К = К₀ .(100 +р)% =12000. 103,5%=12000. 1,035=12420 лв

Б) К = К₀ .(100 +р)% =12420. 103,5%=12420. 1,035=12854,7 лв

.

Задача  :Клиент    вложил в банка 20000 лв на 6 месечен влог с 5% годишна лихва.

А) Колко лева лихва ще получи клиентът  след една година?

Б)Колко лева ще има клиентът в сметката си след една година

Дадено:  :

К ₀  = 20000 лв.

Лихвен срок -  6 месеца ,при годишен лихвен процент – 5%

Лихвени периода ,които ще използва лицето – първи и втори

 Решение

А) Лихвения процент за 6 месеца е 5:2=2,5%

В първия период ,лихвата е проста

20000.2,5% = 500 лева    

Във втория период ,тя вече се капитализира    и е равна на :

(20000 + 500).2,5%  =.20500.0,025 =512,5 лева

Общата лихва е  (500 +512,5) лева    = 1012,5 лева   

Б)   Клиентът в сметката си след една година ше има капитал   К= 20000 +1012,5 =21012,5 лева   

Задача за упражнение  Клиент  внесъл в банка 5000 лв. при годишна лихва 2%. Колко лева ще има клиентът в сметката си след  две години

 Отговор : 5202 лв.

Задача за упражнение   Петър ,внесъл  200000 лв  за 2 седмици ,при лихвен процент за две седмици   0,05% .Колко лева ще получи Петър  

А) в края на първият период  

Б) в края на вторият период  

А) Отговор :  200100 лв.

Б) Отговор :  200200,05 лв.

Задача за упражнение   Фирма внесла   15 000  лв  за  период от 12 месеца ,при лихвен процент  4 %   .Колко лева ще получи фирмата в края на третия период   

Отговор :  16872, 96 лв.

Задача Петър внесъл  в две банки депозити ,като   вторият депозит  е с 2000 лв в повече от първия .Лихвата на първия депозит  е 2 % ,а на втория - 3 % .Ако в края на лихвения период ,Петър е получил от двете банки обща лихва от 455 лв,то намерете ,колко лева е внесъл Петър във всяка банка ?

Решение

Ако   първия депозит означим с  х лв,то  вторият   е  х+2000 лв

Лихвата от първата банка е 2% .х =0,02.х

Лихвата от втората банка е 3% .(х +2000)  =0,03.х  +0,03.2000

От равенството  0,02.х +0,03.х  +0,03.2000 =455 ,намираме,че

0,05х=395,така е х =395 :0,05=7900 лв

Тогава в първата банка са внесени 7900 лева,а във втората 9900 лв

Задача Фирма внесла определена сума в банка на двуседмичен срочен влог, при годишна лихва 12 %. .Ако лихвата в края на месеца е 80 лева,намерете :

А) Колко е лихвения процент  за две седмици

Б) Колко е бил депозита на фирмата

Решение

А) От това,че годишната лихва е 12 % ,то тя е еднаква за всеки месец и е равна на 12:12 =1 %

Един месец има 4 седмици

Тогава лихвата за две седмици  е (1 :4 ).2=0,5 %

Б) Лицето е оставила парите си за два лихвени периода и в края на двата периода е получили лихва 80 лв .

• Лихвата за първия  период е 0,5% .х =0,005.х

Натрупания капитал е х +0,005 .х =1,005  х

• Лихвата за втория период е капитализирана със същите проценти и е равна на

(1,005   х  ) . 0,005 =0,005025.х

• Лихвата за двата периода е 0,005 .х + 0,005025 .х =0,010025.х лв

От  уравнението    0,0125.х.= 80 ,намираме ,че х= 80: 0,010025 =7980 лв(закръглено с точност до десетите)