Урок по геометрия за 7 клас .Еднакви триъгълници.Симетрала и ъглополовяща в триъгълник .Задачи за подготовка за външно оценяване.
ПРОДЪЛЖАВАМЕ С ВТОРА ТЕМА
ВТОРА ТЕМА НА ОНЛАЙН КУРС ПО ГЕОМЕТРИЯ ЗА 7 . КЛАС
|
УЧЕБНА ПРОГРАМА НА ОНЛАЙН КУРС ПО ГЕОМЕТРИЯ ЗА 7. КЛАС
УРОК № 1
ЕДНАКВИ ТРИЪГЪЛНИЦИ .ПРИЗНАЦИ ЗА ЕДНАКВОСТ НА ТРИЪГЪЛНИЦИ
Ако при наслагване предметите съвпаднат ,то казваме че са еднакви. В природата съществува хармония ,основаваща се на еднаквостите.Те са навсякъде ,само трябва да се вгледаме . Създадени безразборно,зад общият им хаос стоят математически модели и формули , описващи точната подредба от еднаквите фигури.
Строители,проектанти,инженери ,дизайнери ,програмисти в ежедневната си работа използват еднаквите фигури . Днес всички те работят със специфични инструменти в графични редактори , с динамични конструкции, като чертаят и програмират cъс софтуер за еднаквост .
Затова в 7 клас започвате изучаването на еднаквите фигури с еднакви триъгълници .
ОСНОВНИ ПОНЯТИЯ И ТВЪРДЕНИЯ Определение Два триъгълника са еднакви, ако съответните страни са равни и съответните ъгли са равни.
|
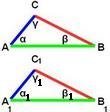
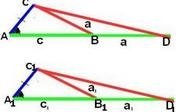
На чертежа Δ АВС и ΔA1В1С1 са еднакви .
Еднаквите страни са оцветени с еднакъв цвят
Запишете съответните ,равни ъгли на <ABC ,<BCA и <CAB
като спазвате правилото срещу равни страни лежат равни ъгли
...........................................................................
Основни задачи - упражнения за входно ниво за първи признак за еднаквост
Задача 1 Като използвате данните от чертежа на квадратната мрежа , намерете всички двойки еднакви триъгълници по първи признак .
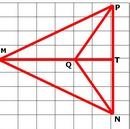
(1)Двойка - Да разгледаме △ MTN и △ MTP От чертежа , следва,че :
PT = TN = 4 cm , <MTN = <MTP=90° а , страната MT =6 cm е обща за двата триъгълника Тогава △MTN ≅ △ MTP по първи признак за еднаквост .
(2) Двойка - Да разгледаме △ MQN и △ MQP От еднаквостта на △MTN и △ MTP ,следва,че : MP = MN , <NMQ =<PMQ а ,страната MQ е обща Тогава △ MQN ≅ △ MQP по първи признак за еднаквост.
(3) Двойка - Да разгледаме △ TQN и △ QTP
От чертежа PT = TN = 4 cm ,<MTN = <MTP=90° а , страната QT е обща за двата триъгълника
Тогава △ TQN ≅ △ TQP по първи признак за еднаквост.
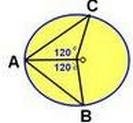
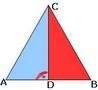
Задача На чертежа е дадена окръжност с център точка О.Опишете :
а) равните елементи по които, △ ACО и △ ABO са еднакви по първи признак
OC e равна на ........... защото са радиуси в окръжност
AO е ….... страна за двата триъгълника
< AOC =............= 120° по условие
b) страната AC е равна ...................защото, лежат срещу равни ъгли от 120 ° в еднаквите триъгълници △ ACО и △ ABO .
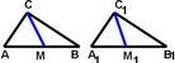
Задача Дадени са два триъгълника ABC и A1B1C1 с медиани съответно CM и C1M1 .
Докажете,че ако CM = C1M1 ,AM = A1M1, и < CMA =< C1M1A1 , то △ ABC ≅ △ A1B1C1
Дадено:
CM = C1M1 ,AM = A1M1 , < CMA =< C1M1A1
Да се докаже,че :
△ ABC ≅ △ A1B1C1
Доказателство
От дадените условия , следва че △ ACM ≅ △ A1C1M1 по първи признак . Тогава всички съответни елементи в двата еднакви триъгълника са равни.
От това,че CM = C1M1 ,то ъглите срещу тях в еднаквите триъгълници са съответни и равни .
Тогава <CAM =<C1A1M1
От това,че < CMA =< C1M1A1 ,то страните срещу тях са съответни и равни .
Тогава AC=A1C1
От това,че AM = A1M1 , то следва че AB =A1B1
Тогава △ ABC ≅ △ A1B1C1 по първи признак ,защото :
AB =A1B1 ,AC=A1C1 и <CAM =<C1A1M1
Втори признак за еднаквост Теорема – признак .Ако страна и двата прилежащи на нея ъгли от един триъгълник са съответно равни на страна и двата прилежащи на нея ъгли от друг триъгълник, то двата триъгълника са еднакви. Втори обобщен признак Ако страна и два ъгъла от един триъгълник са съответно равни на страна и два ъгъла от друг триъгълник, то двата триъгълника са еднакви . |
Основни задачи - упражнения за входно ниво за втори признак за еднаквост
Решение
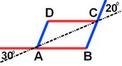
-От това,че AB ІІ CD , то
<CAB =<ACD=30° ,защото са кръстни ъгли
-От това,че AD ІІ BC , то
<ACB =<CAD=20° ,защото са кръстни ъгли
-От това,че AC е обща за двата триъгълника ,то Δ ADC=Δ ABC по втори признак
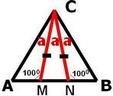
Задача За Δ АВС от чертежа е известно, че CM = CN . Ако <AMC =<BNC=100° и <ACM =<NCB =<MCN=a : Докажете и изчислете :
a)Вътрешните ъгли на △ ABC
b)Δ АMС ≅ Δ BСN
c) АN = BM
Решение
а)За Δ NMС двата външни ъгли са 100 ° ,тогава вътрешните са по 80° градуса . Тогава <MCN= 180° - 2.80° =20° ,така е a=20° и <ACB =3.20°=60°
От Δ АMС следва,че <CAM =180 -100° -20° =60°
От Δ BСN следва,че <NBC =180 -100° -20° =60°
b) Δ АMС ≅ Δ BСN по втори признак
c) Искаме да докажем,че отсечките АN и BM са равни .
Ще търсим триъгълници в които, отсечките са елементи и за които ,можем да докажем,че са еднакви.
Разгледаме двойката триъгълници Δ АNС ≅ Δ BСM Те са еднакви по първи признак ,защото :
AC = CB ,като съответни страни в еднаквите триъгълници АMС и BСN .
CM = CN по условие
<ACN =<MCB =40°
Следователно съответните им елементи са също равни ,така е и третите страни са също равни : АN = BM
Забележка :Равенството на отсечките АN и BM можем,да докажем и без еднакви триъгълници ,като използваме,че от предходната точка сме доказали ,че AM = NB и с добавянето на една и съща отсечка MN получаваме отново равни отсечки ,така е АN = BM
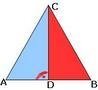
Задача На чертежа CD е височина в ΔАBС , AC = CB и <DAС = < DBC . Докажете,че AD = DB
Дадено :
AC = CB , CD височина в Δ АBС и <DAС = < DBC
Да се докаже,че :
AD = DB
Доказателство
Разглеждаме триъгълниците Δ DAС = Δ DBC в които ,участват отсечките AD и DB
По условие са изпълнени равенствата :
(1)АC =СB
(2)<DAС = <DBC
От това,че CD e височина ,то
<ADС = < BDC=90°
От това,че два от ъглите са равни,то следва ,че и
(3)<AСD = < DCB
От верността на (1) ,(2) и (3), следва,че Δ АDС ≅ Δ DСD
Тогава AD = DB като, съответни елементи в еднакви триъгълници .
Трети признак за еднаквост Ако страните на един триъгълник са съответно равни на страните от друг триъгълник, то двата триъгълника са еднакви. |
Основни задачи - упражнения за входно ниво за трети признак за еднаквост
Дадено :
Фигурата АВСD е правоъгълник
Да се докаже,че :
Δ АВС ≅ Δ АСD
Доказателство
От определението за правоъгълник, следва,че:
АВ =СD
ВС = АD
AС е обща страна за двата триъгълника
За двата триъгълника е изпълнен трети признак за еднаквост на два триъгълника .Следователно Δ АВС ≅ Δ АСD
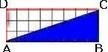
Задача Диагоналът AC на правоъгълника ABCD сключва ъгъл от 30° с BC.Намерете < CAD
Решение От това, че ΔАВС ≅ Δ АСD следва,че всички съответни елементи са равни .
От това,че <ACB=30° и срещу него лежи страната AB ,а AВ = CD в еднаквите триъгълници Δ АВС ≅ Δ АСD ,то съответният ъгъл на <ACB е < CAD.
Тогава < CAD=30° .
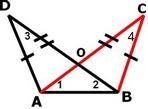
Задача На чертежа АD = BС и DB = AС
Докажете ,че :
a)Δ АDB ≅ Δ ABС
b) <1 =<2 и <3 =<4
c) OD = OСРАЗГЛЕДАЙТЕ ПОПЪЛНЕНИЯТ ТЕКСТ ИЛИ ЧИСЛОВ ИЗРАЗ .В НЯКОЛКО СТЪПКИ СМЕ ПРЕДСТАВИЛИ ВЯРНОТО ДОКАЗАТЕЛСТВО.
a)По условие АD=CB и BD = CA а , AB е обща . Тогава Δ АDB ≅ Δ ABС по трети признак .
b) Търсим съответните елементи по правилото срещу равни страни лежат равни ъгъли . <1 лежи срещу страната BC в триъгълник ABС ,но BC е равна на АD,а срещу АD в триъгълник АDB лежи <2. Следователно < 1= <2
От това,че страната AB е обща за двата еднакви триъгълника и ъглите които ,лежат срещу нея са <3 и <4 ,то следва,че <3 =<4
c)За да докажем,че OD = OС ,отново ще разгледаме подходящи триъгълници ,за които можем да докажем,че са еднакви .Разглеждаме триъгълниците Δ АDO и Δ OBС в които , АD=CB и <3 =<4
От това,че < AOD=<BOC (като противоположни),то АDO ≅ Δ OBС по втори признак . Тогава OD = OС като ,съответни страни лежащи срещу равните ъгли 3 и 4 в двата еднакви триъгълника .
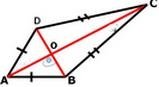
Задача За четириъгълника АВСD от чертежа е известно, че AB = AD и DC=CB и <AOB=90° Докажете ,че BO = DO
ПОПЪЛНЕТЕ ПРОПУСНАТИЯТ ТЕКСТ ИЛИ ЧИСЛОВ ИЗРАЗ .В НЯКОЛКО СТЪПКИ ОПИШЕТЕ ВЯРНОТО ДОКАЗАТЕЛСТВО.
Доказателство
Разглеждаме триъгълниците ADC...........и ............................................
По условие са изпълнени равенствата :
(1)...........................................
(2)......................................................
(3)...........е обща страна ...........................................
Тогава ............................................. по трети признак
Разглеждаме триъгълниците
..........................................................................................................................
в които ,участват отсечките OD и OB
Страната AD =...........................................по условие
От това,че < AOB=90° ,то и <................................ е прав като равни съседни ъгли
< DAO= <..................................., като съответни ъгли в еднаквите триъгълници Δ АDС ≅ Δ ABC
Тогава Δ АDO ≅ Δ ABO по ..............................................................
Тогава OD =OB като, съответни елементи в еднакви триъгълници . (лежат срещу равни ъгли )
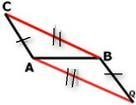
Задача На чертежа АC= BQ и CB= AQ
Докажете ,че :
a)Δ АCB≅ Δ ABQ
b)ACBQ e успоредник
Решение
а) По условие АC=QB и BC = QA а , AB е обща . Тогава Δ АCB≅ Δ ABQ по трети признак . От това,че триъгълниците са еднакви всички останали елементи са равни
b)Знаем,че четириъгълник, чиито срещуположни страни са успоредни, се
нарича успоредник. За да докажем,че AC||BQ и CB||AQ, ще търсим равни кръстни ъгли
-От това,че Δ АCB≅ Δ ABQ,то <ABC = <ВAQ,като съответни лежащи срещу равните страни АC и QB, тогава CB||AQ
-От това,че Δ АCB≅ Δ ABQ,то <CAB= <AВQ,като съответни лежащи срещу равните страни BC и QA , тогава AC||BQ
Следователно , ACBQ e успоредник
Задача В координатна система са дадени точките A( 2,0) , B(3,0) и C(0,2) Програмист трябва да зададе в дадена програма координатите на точка D със свойството : триъгълниците ABC и ABD са еднакви . Помогнете на програмиста с правилното и обосновано изчисление на координатите на точка D.
|
|
|
|
|
|
|
|
| C |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
| B |
|
| O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Четвърти признак за еднаквост Ако две страни и ъгъл срещу по-голямата от един триъгълник са съответно равни на две страни и ъгъл срещу по-голямата от друг триъгълник, то двата триъгълника са еднакви. Признак за еднаквост на правоъгълни триъгълници Ако хипотенуза и катет от единия са съответно равни на катет и хипотенуза от другия, то триъгълниците са еднакви. |
Основни задачи - упражнения за входно ниво за четвърти признак за еднаквост .
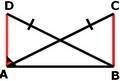
Задача : На чертежа AD ІІ BC ,<DAB =90° и DB = AC
Докажете,че AD = BC
Доказателство
Разглеждаме триъгълниците ABD и ABC
AB е обща
AC = BD по условие
От AD ІІ BC и <DAB =90° , то следва,че и <ABC =90° ,защото сборът от прилежащите ъгли образувани при пресичането на успоредните прави AD и BC с правата AB е 180 °
От признака за еднаквост на правоъгълни триъгълници ,то следва ,че двата триъгълници са еднакви по четвърти признак . Тогава AD = BC като съответни елементи в еднакви триъгълници.
ОСНОВНА ЗАДАЧА
Задача Докажете,че ъглите при основата на всеки равнобедрен триъгълник са равни.
Решение
За да докажем,че ъглите при основата са равни , трябва да ги включим в еднакви триъгълници.
Затова правим допълнително построение .Нека CD е височина към основата на равнобедрения триъгълник. Разглеждаме , триъгълните ADC и DBC . В тях AC = BC, DC е обща и < ADC= <ВDC=90° ,тогава триъгълниците са еднакви по четвърти признак . Следователно съответните им елементи са също равни ,така е < DAC= <DВC (лежат срещу обща страна )
ВАЖНО ! В СЛЕДВАЩИТЕ ЗАДАЧИ ,ЩЕ ИЗПОЛЗВАМЕ ДОКАЗАНОТО ОТ ПРЕДХОДНАТА ЗАДАЧА : АКО ТРИЪГЪЛНИК Е РАВНОБЕДРЕН ,ТО ЪГЛИТЕ ПРИ ОСНОВАТА СА РАВНИ
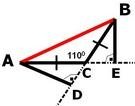
Задача За Δ АВС от чертежа е известно, че CA= CB , а AD и BE са височини съответно към страните BC и AC и <ACB =110° .
а)Изчислете ъглите на триъгълник АВС и триъгълник ABD
b)Опишете още една двойка еднакви триъгълници
c)Докажете,че Δ АDB≅ Δ ABЕ
d)Докажете,че правите AB и DE са успоредни .
а)От това,че AC = BC ,то ъглите при основата са равни , така е <BAC = <ABC .Тогава <ABC =70°:2 и ъглите на ΔАВC са : 35° ,35° и 110 °
От това,че ΔАВD е правоъгълен с ъгъл от 35°, то ъглите му са съответно 90 , 35°и 55 °
b) Триъгълниците ΔАCD и ΔCВE са еднакви по втори признак
АC и ВC са равни по условие ,<ACD =<ВCЕ (като противоположни), <ADB = <BEA = 90°
c)ΔАВD и ΔАВE са еднакви по втори признак ,страните AD и BE са равни ,като съответни от доказаното в подточка b)
d)От еднаквостта на триъгълниците ΔАCD и ΔCВE следва,че CD = CE .Тогава триъгълник CDE е равнобедрен с ъгли при основите равни на 35 ° .
При пресичането си с BD правите AB и DE имат равни кръстни ъгли ,<EDB = < DBA = 35 °
Тогава AB ІІ DE
Задача Едно от твърденията Не винаги е вярно :
Два триъгълника са еднакви ако имат съответно равни :
А) две страни и ъгъл между тях
B) три страни
C) страна и два прилежащи ъгъла
D)три ъгъла
Отговор D)
Задача Ако Δ АВС ≅ Δ МNP и ∠А = 30°, а ∠Р е два пъти по голям от ∠А , то мярката на <B e :
А) 90° B) 50° C) 70° D) 60°
Отговор A)
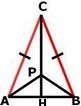
Задача В равнобедрения Δ АВС (АC = BС) точка P е от височината СН. Опишете всички двойки еднакви триъгълници .
Решение
Първа двойка - Триъгълните AHC и HBC са еднакви по четвърти признак
Втора двойка - Триъгълните APC и PBC са еднакви по първи признак
Трета двойка - Триъгълните APH и PBH са еднакви по четвърти признак
Задача В равнобедреният триъгълник ABC (AC = BC ) медианите AM и BN се пресичат в точка O .Докажете,че AO=BO
Задача В равнобедрения △ABC с бедра AC и BC е построена права d успоредна на основата AB .Точка M е произволна точка от правата d, а N е точка от основата AB такава че , MN ІІ AC .Ако точка О е пресечна точка на CB и MN и < BAC= 50 ° , намерете <NOB.
А) 80° B) 50° C) 70° D) 60°
Отговор A)
Задача В равнобедрения △ABC с бедра AC и BC , AD (D e страната BC) и BH (H е от страната AC) са височини към бедрата AC и BC. Ако ∢BAD:∢HBC = 2 : 5, то мярката на ∢ACB е:
А) 10° B) 40° C) 50° D) 60°
Решение
-От това,че ∢BAD:∢HBC = 2 : 5 , то ∢BAD =2x,където x е градусната мярка на един дял , а ∢HBC =5x
-Тогава <ABC=90° - 2x
-От това,че △ABC е равнобедрен ,то височините към бедрата са равни и триъгълниците ABH и ABD са еднакви по втори признак .
-Тогава <ABH =2x ,но по условие ∢HBD=5x
-Тогава 90° - 2x =5x+2x и x=10 °
-Тогава <ABC=90° - 2x=70 ° и ∢BAC= 40 °
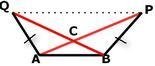
Задача На чертежа Δ ABP ≅ Δ BAQ ,AQ = BP и <PCQ =<130 °. то не е вярно твърдението:
А) AC = BC
B) <CAB= 25°
C) Δ QAC =Δ PBC
D) AB ІІ QP
E)<QAC= 130°
Верен отговор E)
Задача Да се докаже,че ако страна ,прилижащ към нея ъгъл и сумата от дължините на другите две страни в един триъгълник са съответно равни на страна ,прилежащ ъгъл и сумата от дължините на другите две страни в друг триъгълник , то триъгълниците са еднакви .
Дадено :
AC = A1C1
< CAB = C1A1B1
a + c = a1 + c1
Да се докаже ,че : △ ABC ≅ △A1B1C1
Доказателство
На чертежа сме направили допълнително построение ,такова ,че AD = a + c , A1D1 = a1+ c1
Тогава по построение AD = A1 D1
Тогава △ ACD≅ △A1D1C1
Следователно <ADC = <A1 D1C1
От това,че триъгълниците BDC и B1D1C1 са равнобедрени по построение ,то :
<CBA = <C1 B1 A1 (като външни ъгли )
Тогава △ ABC ≅ △A1 B1 C1 по втори разширен признак за еднаквост .
УРОК № 2
СИМЕТРАЛА НА ОТСЕЧКА И ЪГЛОПОЛОВЯЩА НА ЪГЪЛ . СИМЕТРАЛА И ЪГЛОПОЛОВЯЩА В ТРИЪГЪЛНИК И ЧЕТИРИЪГЪЛНИК .
СИМЕТРАЛА НА ОТСЕЧКА ОСНОВНИ ПОНЯТИЯ И ТВЪРДЕНИЯ . Определение за симетрала на отсечка : Правата , която е перпендикулярна на отсечка и минава през средата и се нарича симетрала на отсечка . |
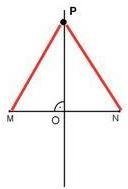
ОСНОВНИ ТЕОРЕМИ Теорема-1.Всяка точка от симетралата е на равни разстояния от краищата на отсечката; На чертежа PM = PN и MO= NO Теорема -2. Всяка точка, която се намира на равни разстояния от краищата на една отсечка, лежи върху симетралата на тази отсечка. Теорема -3.Ако две точки са на равно разстояние от краищата на една отсечка, то правата която ги свързва е симетрала на отсечката |
Основни задачи - упражнения за входно ниво за симетрала в триъгълник и четириъгълник .
Задача .В определението за симетрала на отсечка са пропуснати думи.Запишете ги в пропуснатият текст .
Симетрала на отсечка е (......), която минава през (......) на отсечката и е (.....) на нея.
Задача Даден е триъгълник △ABC ◦ и <) ABC = 80° . Права минава през средата M на BC, перпендикулярна е на BC пресича правата AB в точка P. Да се намери <) CPM.
А) 45° B) 55° C)65° D) 10° Отговор 10°
Упътване :Докажете,че от определението за симетрала , следва еднаквостта на триъгълниците BPM и CPM,като използвате,че в равнобедреният триъгълник ъглите при основата са равни .
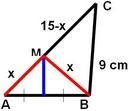
Задача В триъгълник ABC симетралата на АВ пресича страната АС в
точка М. Ако АС = 15 cm и ВС = 9 cm, периметърът на триъгълник BMC е:
А) 20cm B) 24 cm C) 18 cm D) 21 cm
Решение
От това,че точка M е точка от симетралата на отсечката AB ,то AM =MB = x cm
Тогава отсечката CM = 15 – x и периметърът на ΔCBM е :
P = 15 – x + x + 9 ,тогава P =24 cm
Задача ΔABC е равнобедрен (AC = BC) и симетралата на страната BC пресича АС в точка М. Ако AB = 6cm и периметърът на ΔABM е 15cm, то периметърът на ΔABC е:
А) 23cm B) 24cm C) 21 cm D) 24cm
Отговор D)