нови задачи за 6 -ти - 7-ми клас

Задача : (4 точки) Написани са първите 2018 числа, получени по формулата n(n+1 )(n + 2) +1, където n   е естествено число. Колко от написаните числа имат цифра на единиците 1?

А) 2018            Б) 1210             В) 1209           Г) 1211       Д)1009                     

(МАТЕМАТИЧЕСКО СЪСТЕЗАНИЕ „ХИТЪР ПЕТЪР“, 13. 10. 2018 г.,6 кл.)

Решение:

Първите  2018 числа от вида   n(n+1 )(n + 2)+1  са : 

1.2.3+1; 2.3.4+1;3.4.5+1; ........2018.2019.2020+1 

За да завършват на 1 ,то  трябва числата от вида    n(n+1 )(n + 2)   да се делят на 10    

Ако  n   завършва на 5,то n(n+1 )(n + 2) се дели на  10

,като  предходните  две   произведения ,също се делят на 10

Пример: 13.14.15 и 14.15.16 и 15.16.17 се делят на 10

Задачата свеждаме,до намиране на  броя на произведенията от редицата       

3.4.5;4.5.6;5.6.7 ........2015.2016.2017 ; 2018.2019.2020  ,които завършват на 5

От   3.4.5;4.5.6;5.6.7 ........до  2015.2016.2017  те са   (2015:5).3  = 1209

С последното произведение 2018.2019.2020  ,те стават 1210.

Отговор:Б)

Задача.Във всяко квадратче на показаната рамка трябва да се постави по едно число, което да е равно на сбора на двете му съседни числа. Две от числата (10 и 3) вече са поставени. Кое число трябва да се постави на мястото на въпросителния знак?

A)7-     B)3-           C)3       D)7        E)10

(Международно състезание “ Европейско Кенгуру” .17 март 2018 г.Тема 7-8.клас)  

Решение

Има безбройно много числа ,със сбор 10 .Затова ,нека едното събираемо е х .Тогава другото е 10-х

Спазвайки правилото ,следващите числа са : -х ; -10 ; -7

От равенството  -х-7=-10,намираме  че х =3  

В двете посоки ,като прилагаме  правилото ,намираме ,че в квадратчето ,трябва да стои числото 7

Верен отговор :D)

Бележка :В задачата не се изиска да се намери х ,но то трябва да въведе.

Може да откриете отговора и с директна проверка  .

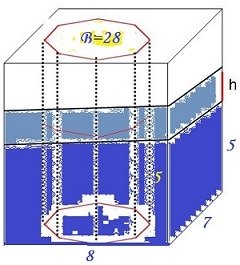
Задача .От квадрат със страна 6 са отрязани 4 правоъгълни триъгълника  с катети 2 ,съдържащи върховете на квадрата ,като е получен осмоъгълник .Осмоъгълникът е основа на права призма с височина 10  .Вана има форма на  правоъгълен паралелепипед  с  височина 10 и  основни ръбове 8 и 7 .Ваната е пълна  до  половината  с вода .Призмата се потапя във ваната ,като основата  ѝ    ляга на дъното .С колко се е повишило , нивото на водата във ваната ?

А)2           Б)3          В)4      Г) 5         Д) никое от тези

 (26-ти Турнир „Черноризец Храбър”,Състезателна тема за 7-8 - ми клас)

Решение :

B_{осмоъгълника} = 6.6- 4.(2.2 :2) =28

Да си припомним:

На всяко тяло, потопено в течност (напълно или частично) действа вертикална сила с посока от долу нагоре и големина, равна на теглото на обема на изместената от него течност.

- Потопеното тяло ,измества  толкова течност , колкото е обемът на

потопената му част

Нека водата във ваната се е повдигнала с  h  единици ,след потапянето до дъното на част  от   осмоъгълната призма

Тогава , обемът на изместената от правилната осмоъгълна призма вода   е.

28.(5+h)

От равенството

7.8. ( h +5) – 7.8.5 = 28.(5+h) ,намираме,че h=5 единици .

Следователно   водата  достига 10 см ,след потапянето на осмоъгълната призма  във ваната .

 Отговор  Г) 

Задача.  Естественото число n се нарича прекрасно  , ако най-големият общ делител на числата n и 100 е 10 , а най-малкото общо кратно на числата n и  84 e 1260 .Колко са прекрасните числа ?

А)0                  Б)1                    В)2                       Г)3

(Математически турнир Иван Салабашев „ ,2017 г ., 6 клас  )

Решение :

(1) От това ,че НОД(n ,100)=10 ,то n е кратно на 10

(2) От  НОК(n , 84)= 1260  ,то съществува естествено число t  ,такова,че :

t.n=1260 = 10.126=10.2.3.3.7

Тогава n e  делител на 10.(2.3.3.7)

От (1) и (2) възможностите за  n са :

n =90, n =630

Отговор В)

Задача . Една баба раздала на трите си  внучета  24 червени  яйца, като всяко получило по толкова яйца, на колкото е години.Най-малкото оставило половината от своите яйца за себе си, а другата  половина разделило по  равно  на   братята  си. След  това  средното  внуче постъпило  по  същия начин с  яйцата, които  вече  имало. Накрая най-голямото направило  същото  със  своите  яйца. В   резултат  се   оказало,че  всяко  внуче  има  един  и  същ  брой   яйца. На  колко  години  е  най-голямото от   внучетата?

А) 14   Б) 10    В)   9   Г) друг   отговор

(Великденско математическо състезание )

Решение

Броя на годините на най-малкото дете се дели на 4

Понеже е най-малко то ,то е по-малко от 8 години

Тогава най-малкото е на 4 години  .Тогава  ,сборът от годините  на другите две деца  е 24- 4 = 20 .

Годините на средното дете са ,такова число ,че след добавяне на 1  се делят  на 4

 Единственото число с това свойство ,по-голямо от 4 и по-малко от 10  е  7

.Тогава средното е на 7 години ,а голямото на 13

Проверка 4,7,13

                  2,8,14

                  4,4,16

                  8, 8, 8

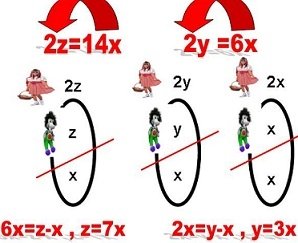
Задача .За да се намери числото a, трябва числото x да се увеличи с 26. Ако x се намали с 26, ще се получи числото -  14. Числото a е равно на:

A) 28       B) 32            C) 36           D) 38               E) 42

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение:                                                                                                                             

Числото х = 26  - 14 =12                                                                                                     

Числото а = 12 +26=38                                                                                                        

 Отговор  D )        

Задача . Кaтя събира 555 групи от по 9 камъчета в една купчина. След това разделя купчината на групи от по 5 камъчета. Колко групи е получила Катя?

 A) 999     B) 900        C) 555          D) 111            E) 45

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение:     

Брой групи  555                                                                                                                          
Брой камъчета 555.9                        

Брой групи по 5 камъчета 

(555.9 ):5=999                                                                                                                                                                                                                                                                                                                                        

 Отговор А )        

Задача В едно училище 60% от учителите отиват на работа с велосипед, а 12% ползват личния си автомобил. Ако учителите, които отиват на работа с велосипед, са 45, колко са учителите, които отиват на работа с кола?

A)    4 B) 6 C) 9 D) 10 E) 12

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

 Решение:      

Ако всички учители  са х броя ,то от това ,че  60% от х са  45  , х =450:0,6=75    

С личен автомобил пътуват   12%  от 75,които са  0,12 .75 =  9  учителя                                                                                                                    

 Отговор  С)

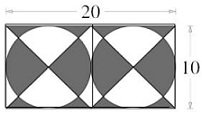
Задача. Намерете лицето на затъмнената част от правоъгълника, който е с размери  20 Х 10 

А) 50    B) 80         C) 100           D) 120          E) 150

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение:   

Фигурата е разделена на два квадрата всеки с лице 10.10=100 кв.единици   .

Във всеки  от двата квадрата , сборът от  лицата от затъмнените малки фигури е  равен на    сборът от  лицата от незатъмнените малки фигури

Тогава  затъмнената част на фигурата има лице   100 :2  +100:2= 100 кв.единици   .

Отговор  С)

Задача. Две въжета, съответно с дължини 1 m и 2 m, са нарязани на части с една и съща дължина. Кое от посочените числа не може да е общият брой на получените части?

A)6    B)8    C) 9    D) 12    E)15

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

   Решение:   

Нека дължината на срязването на въжетата от 1м и 2м е Lм , х и y са съответно броя на частите на които са разрязани въжетата   .

Възможно е   х + y= 6 ,защото :

• L=3:6=0,5м

• 1:0,5=2 броя и 2:0,5=4 броя

Не е възможно е   х + y= 8 ,защото  L=3:8=0,375м , но  1:0,375=2,6(7)  

Отговор  В )

Задача. Миро разполага с 1 червено и 49 сини топчета. Колко топчета трябва Миро да подари на приятеля си Спиро, че 90% от оставащите му топчета да са сини?

A) 4    B) 10         C) 29             D) 39           E) 40

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение: 

Първи начин

Остават 90 % сини и 10 % червени топчета

На 10% отговорят -1 червено топче

На 90%  - 9 сини топчета

Тогава  Миро е дал на Спиро  40 сини топчета

Втори начин  

Нека е дал х сини топчета

От пропорцията (49-х):1=9:1 ,намираме,че х=40

Отговор  Е )

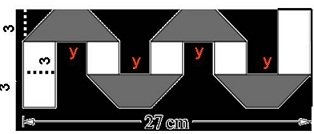
Задача Хартиена правоъгълна лента с широчина 3 см е бяла от едната страна и черна от другата.Лентата е сгъната, както е показано, като са получени четири черни трапеца, три бели квадрата и два бели правоъгълника. Като използвате данните от чертежа, намерете дължината на хартиената лента.

 A)    36 см B) 48 см C) 54 см D) 57 см E) 81 см

Решение :

От това,че  27= 4у+5.3 ,то у =3 см

Тогава при разгъване дължината на линията е   2.2.3+3.3 +4.9  =  57 см

Отговор D  )

Задача. Кенгурчетaта Кенго и Джамбо тръгват едновременно от едно и също място в една и съща посока, правейки всяка секунда по един скок. Скоковете на Джамбо са с дължина 6 м, докато първият скок на Кенго е с дължина 1 м, вторият е 2 м, третият е 3 м и т.н., всеки път скоковете му се увеличават с по 1 м. След колко скока Кенго ще настигне Джамбо?

A)    10    B) 11     C) 12      D) 13      E) 14

(Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение:

Нека след n  скока   Кенго настигне  Джамбо

Пътя на Джамбо е 6. n , а на Кенго  1+2+3+4+....n

Тогава    6. n =  (1+n)n:2 , откъдето намираме,че n= 11

Задачата може да се реши  с директна проверка

Ако n=10 , то пътя до срещата е 60 м .Не съществува n, такова,че 1+2+3+4+....n=60

Ако n=11 , то пътя до срещата на Джамбо  е 66 м  и на Кенго е 1+2+3+4+....11=66 м

Отговор  В)

Задача.  В клас с 20 ученици всички седят по двойки, като точно една трета от момчетата седят с момиче и точно половината от момичетата седят с момче. Колко са момчетата в класа?

A) 9             B) 12                C) 15             D) 16                 E) 18   

 
 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Решение

 Момичетата са четен брой,тогава и момчетата са четен и се делят на 3  

Възможностите са 12 или 18  

Ако са 12  , 12:3=4  и 8:2=4  -имаме 4 двойки момиче с момче,а другите са по двойки само момичета или само момчета 

 Отговор  В)

Задача На черната дъска са записани няколко различни естествени числа. Произведението на двете най-малки измежду тях е 16, а произведението на двете най-големи измежду тях е 225. Намерете сумата на всички числа, записани на черната дъска.

A) 38            B) 42              C) 44                D) 58             E)243

 (Международно състезание “Европейско Кенгуру” 2016 г. ТЕМА за 7 и 8 клас)

Произведението на  двете най-малки измежду тях е 16 =1.16=2.8 

 Произведението на  на двете най-големи измежду тях е 225 = 1.225 =9.25  =  45.5

Тогава сбора от най-малките и най-големите е 2+8+9+25 =  44         

Сбора може да е 44 ,или 58 или 243

Не  е 58 , защото няма числа със сбор 14 ,така,че всяко събираемо да е по-голямо от 8

Не  е 243 , защото няма числа със сбор  199 ,така,че всяко събираемо да е по-малко  от 9 и по-голямо от 8

Отговор  С)

Задача. Четири еднакви правоъгълника, всеки с обиколка 16 см, са разположени, както е показано. Получен е квадрат с квадратна дупка. Намерите обиколката на квадрата.

Задача . Резултатите от четвъртфиналите, полуфиналите и финала на турнир по двойки в някакъв ред са: Борис побеждава Антон, Кирил побеждава Димитър, Георги побеждава Хари, Георги побеждава Кирил, Кирил побеждава Борис, Eмил побеждава Филип и Георги побеждава Eмил. Коя двойка е играла на финала?

A) Георги и Хари       B) Георги и Кирил           C) Кирил и Борис

D) Георги и Емил                 E) Кирил и Димитър

Решение

Георги има три победи –на четвърт финала,на  полуфинала и финала .Тогава е победител на финала

Кирил има  2 победи и една загуба 

Тогава  е играл  на четвърт финала,на  полуфинала и финала  и на финала е загубил от Георги

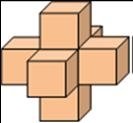
Задача. Показаното тяло вдясно е образувано от седем стандартни зарчета така, че точките върху общите стени са едни и същи. Намерете сбора от точките върху видимите стени на тялото. 

A) 24   B) 90       C) 95         D) 105          E) 126

Решение

Сборът от точките на стените които се допират е 6.7=42 

Сбора от всички точки на 7 -те зарчета е (1+2+3+4+5+6).7=21.7=147

Тогава  сбора от  точките върху видимите стени на тялото  е 147-42=105 т.

Задача:  Четири точки лежат на една права. Дължините на всички получени отсечки в нарастващ ред са 2, 3, k, 11,12 и14. Стойността на k  е

A)5   B)6     C)7     D)9     Е)10

(Математическо състезание „Европейско кенгуру „2015 г.)

Решение  : Нека точките върху правата са  A ,B , C  и D в тази последователност . Тогава отсечките  с дължина    2,3 и k , са  дължини на някоя  от  отсечките  AB ,BC и  CD

Тогава  най-голямата отсечка  AD =  2+ 3+ k =  14 , тогава k=9

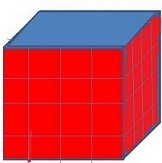
Задача: Васко използвал малки кубчета с ръб 1 см  и  конструирал  куб с ръб 4 см. След това той оцветил три от стените на големия куб в червено, а другите три –в синьо. Оказало се, че няма малко кубче с три червени стени. Колко малки кубчета имат едновременно   синя стена и червена стена?

A)0  B)8   C)12    D)24    Е)32

(Математическо състезание „Европейско кенгуру „)

Решение 

От това,че няма  кубче с три оцветени в червено  стени,то Васко  е оцветявал така ,че трите червени стени да нямат общ  връх .Едно възможно оцветяване е показано на чертежа .

Кубът има 12 ръба ,върху които са разположени кубчетата,  които имат едновременно синя и червена стена .

Започваме да преброяваме кубчетата  с общи  ръбове  от  долната основа

Те са  .4+ 4-1+4-1 =10

Поради симетрията и на горната основа са  също  10  .По околните ръбове има на две места по две  

Отговор D)  24   

 Задача    Няколко различни естествени числа са записани на дъската.Точно две  от тях  се делят на 2  и  точно  13 от  тях се  делят от  13.Ако M е най –голямото от  записаните числа, намерете възможно  най-малката стойност  на М.

 (Математическо състезание "Европейско кенгуру ")

            A)169    B) 260     C)273      D)299       E)325

Решение

Търсим възможно най-малката стойност на М ,ако М е най-голямото записано число .

Ако числата са :13; 2.13;3.13;4.13 ;5.13 ;7.13;9.13;11.13;13.13;15.13;17.13 ;19.13;21.13  ,то  М = 273

Ако съществува по-малка стойност на М ,то ще има повече от две числа ,които се делят на 2   

Задача .Към днешна дата сборът от годините на майката, бабата  и внучката е точно 100. През коя година е родена внучката, ако годините и на трите  са степени на двойката?

A)1998  B)2006   C)2009   D)2010   E)201

Решение

Ако внучката е на 2  години  ,то сборът  от годините на бабата и майката е 98 .Тъй ,като годините им са  едно от числата : 4,8,16,32,64   ,то това е невъзможно .

Ако внучката е на 4 години ,то сборът от годините на  бабата и майката е  96 .Единствената възможност за техните  години е 64 и  32 .Към днешна дата  22март 2014г. ,ако внучката  е родена  от  01.01. 2010  г . до 22 март 2010 г. ,то тя има навършени  4 години

Ако е родена след 22 март ,за да има навършени  4 години  към днешна дата то,тя е  родена  през 2009 година .

Ако внучката е на 8  години  ,то сборът  от годините на бабата и майката е 92 .Тъй ,като годините им са  едно от числата :  16,32 или 64   ,то това е невъзможно .

Не е възможно   внучката  да е по-голяма  от   8 ,защото тогава бабата и майката  ще са на 32 или 64 години .В този случай сборът от годините им е  по-голям от 100

Отговор :

Задача .Намерете броя на всички четири цифрени числа,които се делят на 10.

А) 100     B) 720        C)900      D) друг отговор

Отговор  С)

А)100     B) 800        C)900      D) друг отговор

Отговор  В)

Решение Всички пет  цифрени числа,които се делят на 100 са от вида -  abc00, където  а ≠ 0 .

Техният брой зависи от избора на a, b и c .Тъй като b и c  са едно от числата от 0 до 9 ,то ние можем да ги изберем по 10.10 =100 начина  .На всяко от стоте числа ,съпоставяме  число  от 1 до 9  и получаваме  ,че числата от вида   abc00  са 9.10.10=900  броя

От тях ,ще  извадим  тези,които се делят на  9.

Да преброим тези числа:

Ако с=0 , а  в е цифра  от  0 до 9  ,получаваме числата :00,10,20,30,40,50,60,70,80 и 90

За всяко едно от тези числа ,съществува  точно една цифра а,различна от  нула  , такава ,че сборът от трите числа да се дели на 9 . Получихме  точно  10 числа  900,810,720,630,540,450,360,270,180 и 990

Ако с=1  , в е  цифра  от 0 до 9  ,получаваме числата :01,11,21,31,41,51,61,71,81 и 91

За всяко едно от тези числа ,съществува  точно една цифра ,различна от  нула  , такава ,че сборът от трите числа да се дели на 9 . Получихме  точно  10 числа  -  801,711,621,531,441,351,261,171,981 и 891

……………………………………………………………………………………………………………………………………………………

…………………………………………………………………………………………………………………………………………………..

Ако с=9 , в  е от 0 до 9  ,получаваме числата :09,19,29,39,49,59,69,79,89 и 99

За всяко едно от тези числа ,съществува  точно една цифра ,различна от  нула  , такава ,че сборът от трите числа да се дели на 9 . Получихме  точно 10 числа - 909,819,729,639,549,459,369,279,189 и 999

Така,получаваме,че броят на пет цифрените числа от вида  abc00  , които се делят на 9 са 10.10 = 100

Тогава  пет цифрените числа ,които  се делят на 100  ,но не се делят на 9 са 900 -100 =800 

Задача  Иванчо и Марийка участват в двубой по решаване на тест със 100 задачи. Всеки състезател получава 4 точки за решена задача, ако успее да реши задачата преди противника, или 1 точка за решена задача, ако противникът вече е решил тази задача. Двамата успели да решат по 60 задачи и получили общо 312 точки. Определете броя на задачите, които са решени и от двамата.

A) 53 B) 54 C) 55 D) 56 E) 57

(Математическо състезание "Европейско кенгуру ",2014 година )

Отговор D)

Решение

Нека общо решените от двамата  са y броя  

Нека Иво е решил  x  задачи преди  Мария

За тези задачи той  ще получи  4x+1(y-x)=3x +y  точки

За останалите 60 –y   задачи ,той получава (60 –y).4 = 240 – 4y   точки 

Получихме,че точките на Иво са  3x +y  + 240 – 4y  = 3x -3y  + 240   

За същите задачи  Мария ще получи   1.x+4(y-x)  =  4y- 3x  точки

За останалите 60 –y   задачи ,тя  ще   получи  (60 –y).4 = 240 – 4y   точки 

Получихме,че точките на Мария  са   4y- 3x     + 240 – 4y  = 240 -  3x    

Общо двамата получават  3x -3y  + 240  +  240 -  3x    =312  , откъдето намираме,че y=56

Задача  Капитан Кук и неговият пиратски екипаж задигнали известен брой златни монети, които разпределили поравно помежду си. Ако пиратите бяха с четирима по-малко, то всеки би получил по 10 монети повече, а ако монетите бяха с 50 по-малко, то всеки би получил 5 монети по-малко. Колко златни монети са задигнали капитан Кук и неговият екипаж?

A) 80                     B) 100                    C) 120                      D) 150                  E) 250

(Математическо състезание "Европейско кенгуру ",2014 година )

Верен отговор D) 

Решение

Нека екипажа са x човека и всеки от тях   е получил по  y  броя ,общо xy монети

• Ако пиратите са   x – 4   човека ,всеки ще получи  по  y +10  броя ,общо  (x – 4)( y +10  )  ,които са  също xy  броя 
•   Ако монетите са  xy - 50  ,то всеки би получил  y-5    

Започване с  второто условие :  Ако монетите са  xy- 50 , всеки получава   (xy- 50):x  =  y-5

Тогава получаваме,че x  =10 

• Заместваме в първото условие   и    (x – 4)( y +10  ) = xy и получаваме,че  (10 – 4)( y +10  ) = 10y ,откъдето намираме,че y=15

• Тогава задигнатите монети са  10.15=150 броя

Задача  В три  торби  има  жълъди . В първия   има   6  жълъда ,по-малко  от  сбора на жълъдите в другите два чувала , а във  втория   10 жълъда по-малко  ,отколкото в първия и третия заедно . Колко са  жълъдите в третия чувал ?

Задача . Сборът от три различни двуцифрени положителни числа е 138 . Да се намерят  всички числа , ако едно от тях се дели на 11, едно се дели на 13, а две се делят на 5.                             

Решение

Да разгледаме уравнението

5x + 5y + z = 138

-Ако x се дели на 11 , а  y на 13 , то решенията са 55 ,65 и 18  или 110 , 13 и 15

-Ако x се дели на 11 , а   z  на 13

Тогава  z може да е 13,26,39,52,65,78,91 ,104

Тогава разликата 5x + 5y  е  13 8-13 =125  138-26=112   138-39 =99   138-52=86   138-65 =73   138-78=60     138-91 =47     138-104  = 34  

 Тогава решенията ще търсим от уравненията  5x + 5y  =125  или  5x+ 5y  =60

От това,че  11 / x , то  решенията на първото  уравнение  5x + 5y  =125  ,така е x + y  =25  

са:  x =11 , то y= 14  и числата са 13 ,55  и  70

  От това,че  11 / x , то  решенията на  второто  уравнение  5x + 5y  =60  ,така е x + y  =12   

са:  x =11 , то y= 1  и  получаваме ,че 5.y  е едноцифрено число

-Ако x се дели на 13 , а   z  на 11  

Тогава  z може да е : 11,22,33,44,55,66,77 ,88,99,110,121

Тогава разликата 5x + 5y  е  13 8-11 =127  138-22=116   138-33 =105   138-44= 94  138-55 =83   138-66=72     138-77 =61     138-88  = 50  138-99  = 39   138-110  = 24  138-121  = 27  

 Тогава решенията ще търсим от уравненията  5x + 5y  =105  или  5x+ 5y  =50

От това,че  13 / x , то  решенията на първото  уравнение  x + y  =21  

са:  x =13 ,  y= 8  и числата са 65 ,33  и  40

  От това,че  13 / x , то   второто  уравнение   x + y  =10  няма решение

Не е възможно   z   да се дели на 11 и 13 едновременно ,защото 11.13=143>138

Отговор Решения са тройките числа :(70,55 и 13) , (65 ,40 и 33) ,(  65 ,55 и 18  ) и   (110 , 13 и 15  )                                                                          

Задача  Броят на присъстващите студенти от един курс  на една  лекция  е 4/5  и те са  със  75 повече от  неприсъстващите .Колко  са отсъстващите студенти  на тази лекция?

Решение 

 Нека студентите  от този курс  са x броя .                                                                                                                      Тогава присъстващите са 4/5x,  а отсъстващите  1/5x                                                                                                      От това,че разликата им е 75 ,то съставяме уравнението

                           4/5x -  1/5 x   =75  и    x=125 студента  

Тогава отсъстващите са 1/5 .125 =25  студента       

Задача На състезание                                                                          

Задача. Имам шестцифрена парола  на моята електронна поща.Намерете  моята  парола , ако отговаря на  условията:
(1)Четена отляво надясно и от дясно наляво е една и съща
(2)Номерът е число което се дели на 9
(3) Ако задраскам първата и последната цифра ,ще получа четирицифрено число което е степен на числото  11 .

Решение  Ако   моята  парола  е   записана   с   цифрите  a , b  и  c  то ,от  условие (1) тя ще има  вида

            Разгледам  условие (3)  при което числото 

е  степен  на 11 .Числата  които са степен на 11    са   11,  11.11 ,  11.11.11 ,........

Търсеното число е  четирицифрено   и   се записва  симетрично .

От  всички числа които са степен на числото 11 , само  11.11.11 =1331 отговаря на условията на задачата .Така  намерих   четирите   цифри   на паролата си .

          Не съм  разгледал  условието ,че  номерът е число което се дели на 9 .Знаем,че  за да се дели дадено число  на   9 , то сборът от цифрите му  трябва да се дели  на  9

         От това,че  сборът  на известните цифри  е  1+3+3+1= 8

         Остава да проверя кога числото   2.a +8 се дели  на  9  ,като   a  е число измежду числата  0,1,2,3,4,5,6,7,8   и   9

         Само при   a=5  числото 18 се дели на 9

   Отговор )

Задача Две приятелки Мила и Звездица имат различни играчки за украса за  коледните  си елхи .Общият брой на играчките на двете приятелки е по -малък от  52 .Тази година те решили да си разменят по равен брой играчки .Мила  разделила своите играчки на 5 купчинки  и дала на Звездица 4-те  купчинки ,а  Звездица   разделила  своите играчки на четири купчинки и дала на Мила три от тях  .По колко играчки са си разменили двете приятелки ?

Решение

• ·    Ако във всяка купчинка играчките на Мила са по y играчки , то разменените  са 4y ,общо 5 y
  
• ·    Ако във всяка  купчинка играчките на Звездица са по x броя  , то  разменените са   3x  , общо 4 x
  

Задачата се свежда до намиране на естествените числа , x  и  y   за които 

                                       3x =  4y  и   4x +5y  < 52

От  равенството  правим извода,че  x e число, което се дели на 4  ,  а  y  на 3

Ако x =4 , то y =3  и  разменените играчки са по 12 , общо 24

Тогава  играчките на Звездица  са  4.4=16  , а  на Мила 5.3=15  общо 31

 Ако x =8 , то y =6   и  разменените играчки са по  24  ,общо 48 <52

Тогава  играчките на   5.6=30  , а  на Звезда   32   общо 62>52

                   Единствен верен отговор  - 12,12  общо 31   

З

Задача На чертежа  са дадени  8 точки ,които лежат на две прави .Колко триъгълника можем да  построим с върхове  дадените точки   на чертежа .

 А) 40            B) 30                C) 45                 D) друг отговор 

З

Задача Стоян обича да играе  на компютърът си .   Един ден  той   прострелял  общо 184 картинки  , като  на всяка  игра   прострелял  по равен брой картинки с изключение на една игра.

На  следващия ден  той  прострелял   305 картинки , като в пет от игрите отстрелял с по една картинка  повече от останалите. Ако през двата дни е изиграл ,по равен брой игри , то те са ?

                                            А) 47      B) 61     C) 13    D) 15.

                                                          Отговор B)

Задача На състезание по математика получих верен отговор на 20 задачи .Задачите бяха два вида ,по трудни оценени с 5 точки и по-лесни оценени с 2 точки. Моите точки може да са :

А) 10 B) 50 C) 70 D) друг отговор

Отговор C)

Решение

Нека на x задачи имам по 2 точки .Това са точно 2x точки Тогава на останалита 20 -x задачи ще имам по 5 точки ,или общо 100 – 5x точки . Тогава общият ми брой точки е числото:                                                                                 2x +100 – 5x=100 – 3x точки

• Ако моите точки са 10 ,тогава 100 – 3x =10 и x =30 , но x >20

• Ако моите точки са 50 ,тогава 100 – 3x =50 и 3x =50 , това уравнение няма решение в естествени числа

• Ако моите точки са 70 ,тогава 100 – 3x =70 и x =10 , 10 <20 .Тогава имам 70 точки получени от 10 задачи по 5 точки и 10 задачи по 2 точки

Задача Дължините на две от страните на триъгълник са 10 cm и 4 cm, а периметърът му е цяло число, делящо се на 5. Намерете дължината на третата страна на триъгълника.

А) 11 cm B) 60cm C) 49cm D) 78cm

Отговор A).

Решение

Нека третата страна е a сантиметра .

От неравенствата между страните в триъгълника следва,че a<10+4

Тогава периметърът P=10+4 +a =14+a

От това,че 5/14+a и a<14 cm ,то възможните стойности за a са 1cm,6 cm и 11 cm

Ако a = 1 , то 1 +4 <10

Ако a =6 ,то 1 +6 <10

Следователно само за a =11cm съществува триъгълник с това свойство.

oooo

Задача Правоъгълник  с  обиколка   48 cm е съставен от три еднакви квадрата.Лицето му в квадратни  сантиметри е :

А)36               B) 48                  C)108             D)друг отговор

                                                                Решение 

 Нека измеренията са  a  и  b .

Тогава   a  +  b =24 .Тогава лицето е a.(24-a) =3.x.x  ,  където x е страната на квадрата .От това,че   3  е просто число,следва ,че 3   дели   a   или   24-a ,като и в двата случая  следва ,че 3/a

От това,че   a  +  b =24   и  3/a , следва,че   3/ b

 .Следователно  лицето е кратно на 9  .От това,че 108=3.62 и е кратно на 9 ,то търсеното лице е 108 квадратни сантиметра.

                                                         Отговор C)

Задача Числото 1a2a3a...8a9a се дели на 99. Коя е цифрата a?

А) 1; Б) 3; В) 5; Г) 7.

                        (Математически турнир“Иван Салабашев)

                                                           Решение

Сборът от цифрите на числото е 9a + 45 и от признака за деление на 9 следва,

че то се дели на 9.

За да се дели и на 11 е необходимо числото 9a−45 = 9(a−5) да се дели на11. Това е възможно само при a = 5.

Задача В турнир по футбол участвали 4 отбора,като всеки два отбора изиграли по една среща.

Броят на точките на всеки два съседни по класиране отбори се различават с 1. Колко точки

може да има първият в класирането? (Във футбола за победа се дават 3 т., за реми 1 т. и за

загуба 0 т.)

(Математически турнир „Иван Салабашев“) Решение

От условието следва, че ако първият отбор има x точки, то останалите отбори

имат x−1, x−2 и x−3 точки. Тогава общо точките са 4x−6. Понеже в турнира са изиграни 6

срещи и от всяка среща се получават 3 точки (ако има победител) или 2 точки (ако е завършила

реми), то общо събраните точки са в интервала [12,18]. Следователно 12 ≤ 4x−6 ≤ 18, откъдето

4,5 ≤ x≤ 6. Тъй като x е цяло число, получаваме x = 5 или x= 6. Ако x = 6 в турнира общо

са спечелени 18 точки, което означава, че всички 6 срещи са завършили с победа за единия

отбор. Следователно точките на всеки отбор са кратни на 3, което е невъзможно.

Остава x= 5.