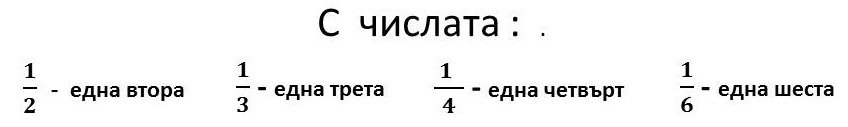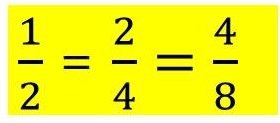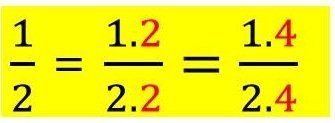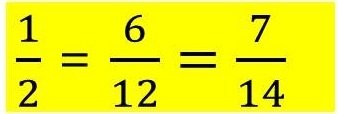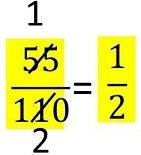Обикновени дроби .Правилни и неправилни дроби .Основно свойство на дробите .Сравняване на дроби .Тестови задачи за 5 . клас
Вие познавате естествените числа -1,2,3 …..N , с които броим и смятаме.
Ако сте петокласник , ние ще ви помогнем с примери и задачи да се научите да четете , пишете и сравнявате обикновени дроби
Съдържание
1.Определение .Четене и писане на обикновени дроби.
2. Основно свойство на дробите : Разширяване и съкращаване на дроб
3.Сравняване на обикновени дроби.
4.Правилни и неправилни дроби
5. Изходно ниво :Задачи за самостоятелна работа
1.Определение .Четене и писане на обикновени дроби.
Ако дадено цяло нещо (ябълка, хляб, окръжност, кръг ,хартия, вестник ) разделим на равни части, то всяка част наричаме дробна единица
Число, образувано от една или няколко еднакви дробни единици, се нарича обикновена дроб .
Пример:
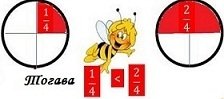
На чертежа ,окръжност е разделена на две , на три , на четири и на шест равни части .
Нека от всяка от четирите окръжности вземем по една част .
означаваме,че от всяка от окръжностите сме взели по една част
1
1.1 Определение за обикновена дроб
Числата от вида
се наричат обикновени дроби
Знаменателят b , ни показва , на колко части сме разделили даденото цяло .Затова b ≠ 0
Числителят a , ни показва , колко части сме взели от даденото цяло
Пример.Обикновената дроб ,която ни показва каква част от правоъгълника е оцветена в лилаво е :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
— - шест петнадесети
15
Числителят е 6 , защото от тези 15 части ,само 6 са оцветени в лилаво .
Пример : Обикновената дроб — петдесет и шест сто и двадесети
120
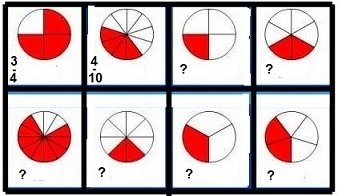
Пример. На картинката са записани обикновени дроби ,които показват каква част от кръга е оцветен в червено
Запишете и произнесете пропуснатите дроби
Пример : Обикновената дроб, която ни показва каква част от километъра са 8 метра е :
8 |
|
1000 |
Пример: Обикновената дроб, която ни показва каква част от денонощието са 3 часа е :
3 |
|
24 |
Пример : Обикновената дроб, която показва каква част от един век са 30 години е :
30 |
|
100 |
Следващите примери са по-сложни ,но много важни за решаване на практически задачи
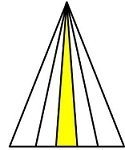
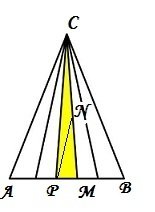
Пример : На чертежа едната страна на триъгълника е разделена на 5 равни части .Получените точки са съединени със срещуположният връх на триъгълника .
Въпрос : Каква част от лицето на големият триъгълник е лицето на триъгълника оцветен в жълто
Отговор :
ВАЖНО ! Щом отсечките са равни , а височината към тях е една и съща , то всички триъгълници имат равни лица
Тогава целият триъгълник е разделен на 5 триъгълника с равни лица
Тогава триъгълника оцветен в жълто, има лице равно на
1 |
|
5 |
Пример : При условията на предходната задача , нека точка N е среда на отсечката СM
Въпрос :Каква част от лицето на триъгълник ABC е лицето на триъгълник PMN
Отговор :
· Триъгълник ABC e разделен на 5 триъгълника с равни лица
· Триъгълник CMP e разделен на два триъгълника с равни лица
· Ако мислено разделим всеки от петте триъгълника ,на два триъгълника с равни лица ,то целият триъгълник ,ще е разделен на 10 триъгълника с равни лица
Тогава триъгълник MNP , има лице равно на
1 |
|
10 |
1.2 Задачи за самостоятелна работа
Упражнение №1 . Дадена е квадратна мрежа ,единичните квадратчета на които са оцветени в различни цветове
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) Запиши обикновената дроб, която показва каква част от квадратната мрежа е оцветена в жълто
|
|
|
Б) Запиши обикновената дроб, която показва каква част от квадратната мрежа е оцветена в зелено
|
|
|
В) Запиши обикновената дроб, която показва каква част от квадратната мрежа е оцветена в лилаво
|
|
|
Г) Запиши обикновената дроб, която показва каква част от квадратната мрежа е оцветена и в лилаво и в бяло
|
|
|
Упражнение 2 .
А) Каква част от кг е един грам
|
Б) Каква част от метъра са 5 см
|
В) Каква част от часът са 12 минути
|
Упражнение № 3 : На картинката големият куб е съставен от 27 квадратчета ,които са оцветени шахматно в бяло и кафяво .
А) Каква част от кубчетата са оцветени в бял цвят
|
|
|
Б) Каква част от кубчетата са оцветени в кафяв цвят
|
|
|
В) Каква част от кубчетата са оцветени и в кафяв цвят и в бял цвят
|
|
|
2. Основно свойство на дробите : Разширяване и съкращаване на дроб
2.1 Разширяване на обикновена дроб
На чертежа една и съща окръжност е разделена съответно на две ,на четири и на осем равни части .
Нека за нас окръжностите са торти
Ако Вие изядете
1 2 4
— или — или —
2 4 8
Затова
Всяка от обикновените дроби ,които са равни се получава ,като числителя и знаменателят на първата дроб се умножат с едно и също число :
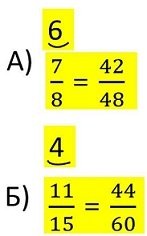
Ако умножим числителят и знаменателят на обикновената дроб
1
-
2 , с 6 и 7 ,получаваме че :
Основно свойство на дробите : Дроб, равна на дадена дроб ,можем да получим ,като умножим числителят и знаменателят на обикновената дроб с едно и също число, различно от нула
Определение : Числото с което умножаваме числителя и знаменателя на обикновената дроб се нарича разширител
Определение : Действието умножение на числителя и знаменателя с едно и също число се нарича „разширяване на обикновена дроб „ :
Примери :
Упражнение №3 :
А) Разширете дадената дроб с 5
4 |
|
5 |
Б) Разширете дадената дроб с 10
7 |
|
20 |
В) Разширете дадената дроб с 0,4
15 |
|
20 |
2.2 Съкращаване на обикновена дроб
Основно свойство на дробите : Дроб, равна на дадена дроб ,можем да получим ,като разделим числителят и знаменателят на обикновената дроб с едно и също число, различно от нула
Определение : Действието деление на числителя и знаменателя с едно и също число се нарича „съкращаване на обикновена дроб „ :
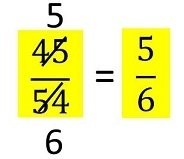
Пример .Дадената дроб съкращаваме с 9 и записваме така
Пример .Дадената дроб съкращаваме с 55 и записваме така
Упражнение №4 :
А) Съкратете дадената дроб с 8
8 |
|
32 |
Б) Съкратете дадената дроб с 7
14 |
|
21 |
В) Съкратете дадената дроб с 10
50 |
|
60 |
Съкратима дроб
Ако числителят и знаменателят на една дроб имат общ делител, дробта се нарича съкратима.
Несъкратима дроб
Ако числителят и знаменателят на една дроб нямат общ делител, дробта се нарича несъкратима.