Прав кръгов конус .Задачи от лице на повърхнина и обем на прав кръгов конус за 6 клас .
Съдържание:
1.Прав кръгов конус .Елементи и получаване на прав кръгов конус .
2.Развивка на прав кръгов конус . Лице на повърхнина на прав кръгов конус .Основни задачи за 6 клас
3. Обем на прав кръгов конус.Основни задачи за 6 клас
4.Избрани задачи за 7 .клас ( закон на Архимед )1
1.Прав кръгов конус .Елементи и получаване на прав кръгов конус .
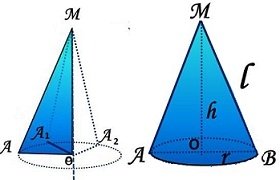
Чертеж 1 Чертеж 2
На чертеж 1 е даден правоъгълен триъгълник AOM с катети AO и OM и хипотенуза AM
Правим пълно завъртане на този триъгълник , около катетът му ОM
В резултат на завъртането :
- катетът АО описва окръжност с център т. О, защото OA =OA1 =OA2 ....
- хипотенузата АM описва повърхнина ,в която MA =MA1 =MA2 ....
На чертеж 2 е дадено тялото ,което се получава в резултат на завъртането на този правоъгълен триъгълник
Всяко валчесто тяло получено по този начин се нарича прав кръгов конус
Основните елементи на всеки прав кръгов конус са :
- Точката М - ВРЪХ на конуса
- AM =BM = l - ОБРАЗУВАЩА на конуса
- AO =OB = r - РАДИУС на конуса
- MO = h - ВИСОЧИНА на конуса
- Кръгът с диаметър АB се нарича ОСНОВА на конуса
Част от елементите на всички предмети на картинката имат форма на прав кръгов конус
1. задача Попълнете липсващият текст
А) Кръгът получен от завъртането на правоъгълен триъгълник ,около един от катетите му , наричаме (………) ,а радиусът му r ,наричаме (……………………)
Б) Другият катет на правоъгълният триъгълник ,който завъртаме се нарича (…….) на конуса и се бележи (……)
В)Коничната повърхнина ,която описва една образуваща се нарича (………………….)
Г) Отсечката МО,която лежи на правата около,която въртим правоъгълника се нарича (…………) и се бележи с (……)
2.задача Даден е правоъгълен триъгълник с катети а= 6 см , b= 8 см и хипотенуза с= 10 см
А) Ако го завъртите , около катета а=6 см ,то намерете дължините на неговите елементи- r , l и h
Б) Ако го завъртите , около катета b= 8 см , начертайте в квадратна мрежа полученият прав кръгов конус
2.Развивка на прав кръгов конус
Всеки предмет от нашето ежедневие с форма на конус е, или сглобен или излят в специална форма.
Ако предметът е сглобен, то той е създаден като :
- се начертаe неговата развивка
- се съединят нейните части – основа и околна повърхнина
- се изчисли лицето на повърхнината на получената развивка
- се пресметнат всички разходи за единица продукт: проектиране,материали ,разходи за боядисване или облепване,човешки ресурс
Затова е важно всеки от Вас да познава развивката на конус ,от която се намира формула за лице на повърхнината му
На тази страница от нашият сайт са направени подробни обяснения за чертане на развивка на конус
Тук са изведени и всички формули за лице на повърхнина на конус
1
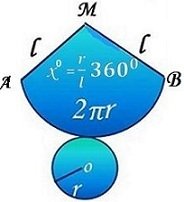
На чертежа е дадена развивката на конус с радиус r , образуваща l и конична повърхнина - фигурата AMB
Упражнение :Намерете ъгълът между образуващите AM и MB в развивката на прав кръгов конус с радиус r =3 см и образуваща l =5 см
Формула за лице на околна повърхнина на прав кръгов конус
S= п.r.l |
Формула за лице на повърхнина на прав кръгов конус
S 1 = S + B , където В = пr2 |
S 1= пrl + пr2 = пr(l+r) |
Основни задачи от лице на повърхнина на конус за 6 клас
3.задача Даден е прав кръгов конус с радиус равен r= 2,5 дм и образуваща l= 8 дм
А) Намерете лицето на околната повърхнина на конуса
Б) Намерете лицето на повърхнина на конуса
В) Колко най-малко листа гланцова хартия ще ни трябват за облепването на конуса ,ако гланцовите листа имат форма на правоъгълник с размери 20 см и 30 см
Решение
А) S =пrl =3,14 .2,5.8 ==62,8 дм2
Б)За по - бързи изчисления ,заместваме дадените елементи в кратката формула за лице на повърхнина на конус и намираме,че :
S1=пr.(l + r) =3,14.2.5 (8+2,5 )= 81,375 дм 2
В) Един гланцов лист с форма на правоъгълник с размери 20 см=2 дм и 30 см =3 дм има лице 2.3=6 дм2
От това,че облепваме целият конус , работим с лицето на повърхнината му.
От това,че 81,375 :6 = 13,56 , то ще ни трябват най-малко 14 броя гланцови листа
.
4.задача Намерете лицето на околната повърхнина на конус , ако радиусът на основата му r = 10 дм, а образуващата му l е 150 % по-голяма от него
Решение
S =пrl =3,14 .10(10+1,5.10)=785 дм2
5.задача Радиусът на цилиндър е с 80% по-малък от образуващата му l= 150 см .Намерете лицето на повърхнината му в квадратни дециметри .
Решение
От l = 150 см = 15 дм , то r = 15 – 0,8.15 =3 дм
S1=пr.(l + r) =п.3 (3+15)= 54п дм2
6.задача Лицето на околната повърхнина на конус е 356.п см2 ,а радиусът му е 8 см .Намерете образуващата на цилиндъра .
Решение
S=пrl |
Тогава
356 π = π . 8. l |
Тогава
356 = 8. l ,откъдето l =356 : 8=44,5 см |
7.задача Лицето на основата на прав кръгов конус е равно на 49 п дм, а образуващата му l = 8 дм .Намерете лицето на повърхнината му .
Решение
За да намерим лицето S1=пr.(l + r), трябва да намерим r
От условието B =пr2 =49 п , намираме,че r = 7 см
Тогава S1=пr.(l + r) =п.7 (7+8)= 105п дм2
8.задача Лицето на повърхнината на конус е 234 п см2 ,а радиусът му е 12 см .Намерете образуващата на цилиндъра
Решение
S1=пr.(l + r) |
Тогава
234п=п12.(l + 12) |
Тогава
234 = 12.(l + 12 ) |
Тогава
l + 12= 234 :12 =19,5 см |
Тогава
l =19,5 -12= 7,5 см |
9.задача Лицето на основата на прав кръгов конус е равно на 81п и е 2 пъти малко от лицето на околната му повърхнина .Намерете образуващата му .
Решение
От условието B =пr2 =81 п , намираме,че r = 9 см
От условието 2B= S ,след заместване с дадените елементи получаваме равенството :
2.81п= п.9.l, от което намираме,че l= 18 дм
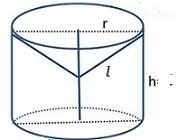
10.задача От цилиндър е издълбан конус , така както е показано на фигурата .
А) Ако радиусът на цилиндъра r , е равен на 5 см , а образуващата на конуса l има дължина равна на 6 см , и тя е половината от височината на цилиндъра , то намерете лицето на повърхнината на полученото тяло
Б) Ако образуващата на конуса е 5 см, а образуващата на цилиндъра е 12 см и лицето на повърхнината на конуса е четири пъти по –малко от лицето на повърхнината на цилиндъра,то намерете радиусът на цилиндъра
Решение
А ) След издълбаването на конуса ,се получава тяло ,чиято повърхнина е равна на
S тялото = S цилиндъра + В цилиндъра + S конусът
S тялото = 2пr.(2l) + пr2 + пr.l =5 пr.l + пr2
S тялото = 5п5.12 + п25 =325 п
Б) От S1 цилиндъра = 4S1конуса
получаваме,че 2пr.(12 + r) =4пr.(5 + r)
Тогава 12 + r =2(5 + r)
Тогава , 12 + r =10 + 2r , откъдето намираме,че r =2 см
11.задача Радиусите на основите на два конуса са равни на 6 cm, а образуващите им на 9 cm и 12 cm. С колко процента лицето на околната повърхнина на единият конус е по –голямо от лицето на околната повърхнина на другият конус .
Решение
S = π . r . l
S = π .9.6
S = 54. π см 2
S = π .6. 12
S = 74. π см 2
Търсим (54. π : 74. π) :100% =73% (закръглено с точност до стотните)
12.задача Сборът от дължините на радиуса и образуващата на конус е 12 см, а лицето на пълната му повърхнина е 48 π см3. Да се намери радиусът на конуса
Решение:
r + l = 12
S1 = 48.π
π.r(r + l) = 48.π
r.(12) = 48
r= 48:12=4 см
От r < l , то този конус съществува
Задачи за самостоятелна работа от лице на повърхнина на конус
13.задача Намерете образуващата на конус с радиус на основата 10 см и лице на повърхнината му 1177,5 см 2
Отговор : 27,5 см
14.задача При завъртането на правоъгълен триъгълник ,около един от неговите катети се получил прав кръгов конус с образуваща , равна на 60 см и лице на околната повърхнина 376,8 см2. Намерете другият катет на правоъгълният триъгълник .
Отговор : b= 2 см
15.задача С колко процента ще се увеличи лицето на околната повърхнина на конус , ако радиусът му се увеличи 8 пъти
Решение
Прав кръгъв конус с радиус r и образуваща I има околна повърхнина S=пrl
Прав кръгъв конус с радиус 4r и образуваща I има околна повърхнина S=п8rl =8пrl
Увеличението на околната повърхнина в проценти е :
(пrl : 8пrl).100% = 12,5 %
16.задача С колко процента ще се увеличи лицето на околната повърхнина на конус,ако височината му се увеличи от 9 см на 12 см;
Отговор : 75 %
17.задача.Намерете лицето на повърхнината на конус, ако околната му повърхнина е 84.п см2, а образуващата му е 24 см.
Отговори 96,25 п см2
18.задача Прав кръгов конус има образуваща l см , радиус r см ,дължина на окръжността на основата C см , лице на околна повърхнина S см 2 и лице на повърхнината си S1 см2
Попълнете таблицата
| r | C | l | S | S1 |
Първи случай | 6 |
|
| 132 п |
|
Втори случай |
| 24п |
| 168п |
|
Трети случай |
| 12п |
|
| 240п |
|
|
|
19.задача Отвес има форма на прав кръгов конус с диаметър d =16 см и образуваща l = 2,5 дм .Ако за боядисването на 1 кв.дм са необходими 300 грама боя , то намерете колко кг боя е необходими за боядисването на целият отвес.
Отговор : 1,884 кг
20.задача :Малка дизайнерска фирма има поръчка да изработи 100 шапки с форма на конус с обща цена 200 лева .Разходите за материали са 80% от всички разходи и в тях са предвидени 15% резерви . Ако радиусът на шапката е 6 см и един кв.метър от материала за шапки е 0,02 ст ,то намерете :
А) образуващата на конуса .Изчисленията направете с точност до стотните .
Б) Ако не е възможно фирмата да изпълни такава поръчка , обосновете отговорът си .
21.задача Радиусът на конус е 2 см. Лицето на повърхнината на конуса е три пъти по-голямо от лицето на основата му. Да се намери дължината на образуващата на конуса.
Отговор:) l = 4 см
3. Обем на прав кръгов конус.Основни задачи за 6 клас
За да получим формула за намиране на обем на конус ,ще използваме знанията си за обем на цилиндър .
Ние знаем,че обемът на всеки цилиндър , намираме с формулата .
Vцилиндър = B.h , където В =п.r2 ,а h е височината на цилиндъра |
Ще покажем с опит ,че обемът на всеки конус се намира с формулата :
B.h |
Вземаме цилиндър и конус , които имат :
- Равни височини h
- Равни радиуси r
Напълваме тялото с форма на конус с течност или материал и го пресипваме в съда с форма на цилиндър
Точно след три пресипвания цилиндъра се напълва догоре
Това ,ни показва,че обемът на конусът а е третината от обемът на цилиндъра .
Тогава обемът на всеки конус с радиус на основата r и височина h , намираме с формулата
п.r2.h |
22 .задача Обемът на цилиндър е равен на 300 см3 .Намерете обемът на конус ,който има радиус на основата и височина равни на радиусът на основата и височината на цилиндъра
Решение
1
Vконус = —— Vцилиндър
3
1
Vконус = —— 300 = 100 см3
3
23 .задача Намерете обемът на конус с радиус r и височина h , ако :
А) r = 10 см , h=2 дм
Б) r = 1 м , h=200 дм
С) r = 20 мм , h=,08 м
24 .задача Тяло има форма на конус с радиус на основата r = 0,5 дм и образуваща l = 5,4 дм .Намерете с колко милилитра вода може да се напълни това тяло ?
Решение Търсим вместимостта на конуса в милилитри .
1 милитър = 1 куб.сантиметър |
Тогава работим в сантиметри - r = 0,5 дм = 5 см ,а l = 5,4 дм =54 см
п.52.54
V = —— = 4239 см3 = 4239 милилитра
3
25.задача Как ще се измени обемът на конус, ако:
А) радиусът му се увеличи три пъти;
Б) височината му се увеличи три пъти;
В) радиусът му се намали четири пъти, а височината му се увеличи 4 пъти.
Решение
r2.h
А) Ако V = —— , с увеличаване на радиусът му три пъти ,обемът вече е равен на
3
V = —— , което ни показва ,че той се увеличава 9 пъти
3
26.задача Вместимостта на съд с формата на конус е 9420 литра. Ако радиусът конуса е 3 м, намерете височината на съда.
Решение
1 литър = 1 куб.дециметър r = 3м = 30 дм 9420 литра = 9420 дм2 |
пr2.h
От V = —— , получаваме равенство за височината h
3
р
п9.h
9420 = —— , от което намираме,че 9420.3 = 3,14.9h и h = 1000 дм
3
27 .задача Намерете обемът на конус с височина h=40см , образуваща l =50 см и лице на околната повърхнина S=1500п см2
Решение
S = n.r .l
1500n = n . r . 50
r = 30 см
V = ( n.r2 . h ) : 3 = (n .302.50) : 3
V = 15 000 n см328.задача Прав кръгов конус с височина h = 2 дм има обиколка на основата С = 3п дм и лице на повърхнина S1 =6п дм2 Намерете :
А) радиусът r и образуващата l
Б) Обемът на конусът
Решение
А)
От С=2пr , то 3п = 2пr , откъдето намираме,че r = 1,5 дм |
S1=пr(r+l) |
Тогава
6п = п1,5(1,5 + l) |
Тогава
(1,5 + l) = 6:1,5, |
Тогава
l = 4-1,5=2,5 |
Б) Отговор 1,5п дм3
29 .задача Попълнете таблицата
| r | C | ‘B | l | S | h | S1 | V |
Първи случай | 2 |
|
|
| 40 п | 5 |
|
|
Втори случай |
| 24п |
|
|
|
| 324п | 1296п |
Трети случай |
|
|
|
| 60п | 8 | 96п |
|
|
|
|
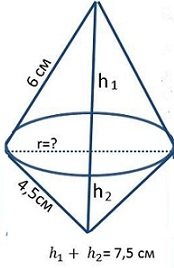
.
30.задача Даден е правоъгълен триъгълник с катети а = 4.5 см , b=6 см и хипотенуза c = 7,5 см .Ако го завъртим , около неговата хипотенуза ,ще получим тяло ,което е съставено от два конуса .Намерете :
А) височината към хипотенузата на даденият правоъгълен триъгълник
Б) обемът на тялото
В) лицето на повърхнината на тялото
А ) Изразяваме лицето на правоъгълният триъгълник по два начина :
- чрез катетите му а и b
- чрез хипотенузата му c и височината към нея (r )
Получаваме равенството (аb) : 2 = (с hc) : 2
След заместване с дадените елементи , получаваме равенство за hc
(4,5.6) : 2 = (7,5 . hc ):2 , от което намираме,че hc = 3,6 см
Б) За да намерим обемът на тялото ,което е съставено от два конуса с обща основа , то ние трябва да намерим радиусът на основата
Радиусът на основата r e равен на височината hc на даденият правоъгълен триъгълник
Обемът на тялото e сбор от обемите на двата конуса и е равно на :
п.3,62 h1 п3,62 h2
V= —---- + ———---
3 3
п3,62.(h1 +h2)
V = ———-------- = 32,4п см3
3
В) Отговор : 37,8 см2
31.задача На чертежа са дадени размерите на пастел за рисуване .Намерете :
А) обемът на тялото на чертежа
Б) колко милиграма тежи пастелът за рисуване,ако 1 куб.см тежи 0,002 грама .
Упътване : 1 mg = 10-3g = 10-6kg
Отговори А) 41,7 см3 Б) 94,2 милиграма
32.задача .От метално тяло с форма на куб с ръб равен на 10 см е изрязан прав кръгов конус с възможно най-голям радиус и височина ,която е третината от височината на кубът .Ако кубът тежи 3 кг , то намерете :
А) теглото в грамове на един кубичен сантиметър
Б ) обемът и теглото на конуса
Резултатите закръглете с точност да стотните
33.задача Прав кръгов конус с височина h = 2 дм има лице на повърхнината S 1 =6 п дм2 и лице на околната повърхнина S = 3,75п дм2 .Намерете обемът на цилиндъра
Решение
S1=В+ S |
Тогава
6п = пr2 + 3,75п |
Тогава
пr2 = 6п-3,75п |
Тогава
пr2 = 2,25п |
Тогава
r2=2,25 дм , откъдето намираме,че r= 1,5 дм |
V = (п.1,52 .2) : 3 =1,5 п дм3 |
34 .задача От прав кръгов конус е изрязана правилна четириъгълна пирамида с основен ръб 3см и височината 5см. Ако височините на двете тела са равни и обемът на полученото тяло е 100 см3 , то намерете обемът на конусът .
Отговор : 115 см3
4.Избрани задачи за 7 .клас ( закон на Архимед )
35 .задача В чаша за мартини с форма на конус с вместимост от 224 милилитра се поставят по 3 бучки лед с форма на куб с ръб от 2 cm и се пълни чашата догоре със сок .Ако бучките лед са на дъното на чашата , то намерете, количеството сок в милилитри , с което трябва да се напълни чашата ,без да прелее
Решете задачата като използвате извод от известен закон от физиката ,носещ името на Архимед ,който гласи : Ако тяло е по-тежко от течността, в която e потопено, то потъва до дъното и измества течност с обем равен на обема на потопеното тяло
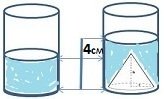
36.задача В чаша за вода с форма на цилиндър с радиус 3 см има известно количество вода .На дъното на чашата се поставя метален конус с радиус равен на радиуса на цилиндъра .След поставянето му в чашата нивото на водата се повдига с 4 см .Намерете височината на металният конус .
Решение
Изразяваме обемът на конуса по два начина:
- От условието на задачата и от закона на Архимед , получаваме,че обемът на конусът е равен на обем на цилиндър с радиус r =3 и височина 4 см .Тогава ,той е равен на п32 4 = 36 п
- Обемът на конус с радиус 3см и височина h, е равен на ( п32.h) :3
Тогава е вярно равенството ( п32.h) :3== 36п , от което намираме,че h=9 см